На этом шаге мы рассмотрим анализ сложности рекурсивных алгоритмов.
Рассмотрим сначала случай прямой рекурсии с единственным (вне какого-либо цикла) рекурсивным вызовом в теле процедуры. Примером такого алгоритма является алгоритм Евклида вычисления наибольшего общего делителя.
Напомним, что текст рекурсивной процедуры с вектором исходных данных X содержит вызов этой же процедуры с измененным по некоторому правилу вектором исходных данных Y = f(X). Кроме этого, в тексте содержится некоторое нерекурсивное вычисление h(X) и операции сравнения c(Х,S) значения X со значением S, при котором рекурсивный процесс должен заканчиваться. Обозначим "точное" (а не верхнюю границу или среднее) значение сложности при входных данных X через Тα(X). Тогда
Тα(X) = Тα(Y) + Th(X) + Tc(X,S),
или
Тα(X) = Тα(АХ)) + Tf(X) + Th(X) + Tc(X,S).
Второе соотношение представляет собой рекуррентное уравнение для определения значений неизвестной функции Тα(X) через известные значения f(A), Tf(X), Th(X), Tc(X,S). Кроме этого, имеется начальное условие Tα(S)=Ts(S) с известной функцией сложности вычисления (нерекурсивного) значения S. Таким образом, имеется система:
Тα(Х) =Tα(f(X))+ Tf(X)+Th(X)+ Тc(X, S) Tα(S)=Tc(S,S)+Ts(S)
Это частный случай рекуррентного уравнения. Такие уравнения имеют развитую теорию. В некоторых случаях возможно аналитическое решение. Покажем его применение на примере рекурсивного вычисления факториала:
function FACTORIAL (х: integer): integer; begin if x = 1 then FACTORIAL:= 1 else FACTORIAL:= x * FACTORIAL (x-1); end;
Здесь X = x, S = 1, f(X)=X-1, Tf(X)=1, Th(X) = 2, Tc(X,S)=l, Ts(S) = 1. Таким образом, система уравнений превращается в
Тα(x) = Тα(х-1)+4, Тα(1) = 2.
Ее решение - Тα(x) = 4х-2.
Верхняя оценка Тα(V) может быть получена подобным образом, но с использованием рекуррентных неравенств:
Тα(V) <= Тα(f(V))+Tf(V)+Th(V)+Tc(V,V0), Tα(V0) <= Tc(V0, Vo)+Ts(V0).
Оценка среднего значения сложности требует учета вероятностных законов и может быть значительно более трудной. Вообще говоря, нельзя использовать написанные выше рекуррентные уравнения в вероятностном случае: среднее значение функции случайной величины не равно значению функции от среднего значения случайной величины,
среднее (f(X)) <> f(среднее (X)),
кроме случая линейной функции f.
Теперь рассмотрим более общий случай прямой рекурсии с несколькими рекурсивными вызовами в теле процедуры. Эти вызовы могут иметь разные аргументы Y1, Y2, . . . ,Yk, где Y1 =fl(X), Y2 =f2(X), ..., Yk=fk(X). Рекуррентное уравнение для функции сложности имеет вид
Тα(X) = Тα(f1(X)) + Тα(f2(X)) + ... + Тα(fk(X)) + Tf1(X) + Тf2(X) + ...+
Тfk(X) + Тh (X) + Tc (X, S)
Тα(S) = Tc (S, S) + Ts (S).
В реальных рекурсивных алгоритмах встречаются различные функции fi(X), однако, подчиняющиеся обычно определенным закономерностям. Эти наиболее часто встречающиеся случаи мы сейчас рассмотрим.
1. Одинаковые функции fl(X) = ...= fk(X) = f(X). Рекуррентное уравнение для функции сложности имеет вид:
Тα(X) = k Тα (f(Х))+kTf(X)+Th(X) + ТС(Х, S),
Tα(S)=Tc(S,S)+Ts(S).
Решение этого уравнения зависит от соотношения k и f(X). Ясно, что если k > 1, то значения Tα (X) быстро возрастают с ростом X (если значения могут быть упорядочены) или Tα (V) быстро возрастают с ростом V, если функция f недостаточно быстро уменьшает X. Первый пример как раз такого рода: k = 2, f(X)=Х-1.
Проведем анализ решения известной головоломки "Ханойская башня" (рисунок 1) - игры, основанной на древнем ритуале брахманской башни, с помощью которого, по преданию, брахманские жрецы предсказывали конец света.
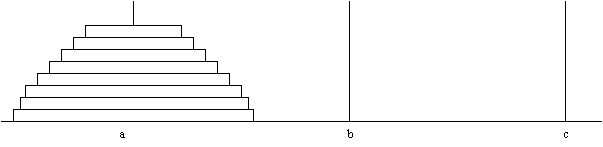
Рис.1. Ханойская башня
Задача состоит в следующем.
Имеется три алмазных иглы: a, b, c. В момент творения на иглу а нанизываются 64 золотых диска уменьшающихся размеров (будем рассматривать задачу для n дисков). Все диски имеют разный диаметр, внизу находится самый большой диск, а наверху - самый маленький. Никакой диск большего диаметра не может находиться выше диска меньшего диаметра. На иглах b и с дисков нет. Перед брахманскими жрецами, только что посвященными в сан, ставится задача переложить диски на иглу b. При этом иглой с можно пользоваться как временной емкостью. Конец света наступит, когда все 64 диска окажутся на игле b в том же порядке, в котором они располагались на игле a.
С алгоритмической точки зрения элементарным шагом является перенос одного диска. В задаче имеется важное ограничение: ни на одной из игл никогда не должно возникать ситуации, при которой диск большего диаметра лежит на диске меньшего диаметра.
Рекурсивное решение этой задачи выглядит естественно и просто. Пусть процедура CARRY (n, а, b, c) переносит башню высоты n с иглы а на иглу b, используя иглу c как вспомогательную. Тогда исходная задача может быть разбита на три части:
CARRY (n-1, а, с, b) {Перенести верхние n-1 дисков на с.} CARRY (1, а, b, - ); {Перенести один (нижний) диск на b.} CARRY (n-1, с, b, а);{Перенести башню с c на большой диск, уже находящийся на b.}
Вторая часть тривиальная, одношаговая. Выделим ее в отдельную нерекурсивную процедуру ONEDISK (a,b). Теперь можно написать рекурсивную процедуру:
procedure CARRY (n, а, b, c: integer); begin if n > 1 then begin CARRY (n-1, а, с, b); ONEDISK (a,b); CARRY (n-1, c, b, a) end; end;
Сложность процедуры ONEDISK - константа (обозначим ее K). Входной набор Z = (n, а, b, с). Достаточно очевидно, что номера игл а, b, с никак не влияют на сложность. Поэтому можно принять V = n. Рекурсивное уравнение примет вид:
Тα (n) = 2Тα (n-1) +2 + h + 1, Тα (1) = 1 + 0, или Тα (n) = 2Тa (n-1) + h + 3, Тα (1) = 1.
Решение этого уравнения может быть получено в виде:
Тα (n) = v 2n + w,
где v, w - параметры, подлежащие определению.
Уравнения для определения v и w получаются из предыдущих рекуррентных соотношений:
v2n + w = 2v2(n-1) + 2w + h + 3, v2 + w = 1
Итого,
Tα (n) = (2 + h/2) 2n - (h + 3).
Найденная оценка сложности относится к классу так называемых экспоненциальных функций временной сложности.
Второй тип рекуррентных уравнений, часто встречающихся в анализе алгоритмов, может быть задан следующими формулами:
Tα (V) = k Tα (V/m) +lV, Тα (1) = l,
при этом предполагается, что сложность данных V - натуральное число.
При отсутствии явного выражения решения в виде формулы, включающей элементарные функции, обычно удовлетворяются асимптотическим решением, т. е. приближенной формулой, точность которой возрастает с ростом V.
Асимптотическое решение уравнений этого типа будет следующим:
Тα (V) = О (V), если k < m, Тα (V) = О (V logV), если k = m, Тα (V) = О (V logmk), если k > m.
2. Функции, образующие прогрессию Х-1, Х-2, ..., Х-k.
Пример такой процедуры для k-2 уже был приведен - рекурсивная процедура для нахождения n-го числа Фибоначчи. Проведем более детальный ее анализ.
function Fr (n: integer): integer; begin if n = 1 or n = 2 then Fr := 1 else Fr := Fr(n-1) + Fr(n-2); end;
Здесь сразу можно взять Х= n, Tf1(n) = Tf2(n) = 1, Th (n) = 2, Тс(n) = 2, Ts (n) = 1. Уравнения для функции сложности: Тα (n) = Тα (n-1) + Тα (n-2) + 6, Тα (2) = 3, Тα (1) = 3.
На следующем шаге мы рассмотрим случай косвенной рекурсии.
