На этом шаге мы рассмотрим построение функции сложности по управляющему графу, содержащему циклы while или repeat.

Управляющий граф содержит цикл, порожденный операторами while или repeat

    Циклы while и repeat анализировать сложнее, чем оператор for, так как количество исполнений тела цикла зависит от истинности или ложности условия и, может быть, достаточно сложных изменений в теле цикла значений переменных, входящих в состав условия.

    Рассмотрим в качестве примера вычисление методом Ньютона (имеется в виду вычисление вещественного значения корня). Задача сводится к нахождению корня уравнения x^(1/p) - z = 0, который, в свою очередь, отыскивается с помощью итерационного процесса

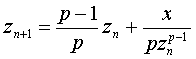
начинающегося некоторым начальным значением z₀, выбираемым возможно наиболее близким к корню. Окончание процесса происходит, когда корень оказывается найденным с заданной точностью ε с помощью, например, следующей функции.

function P_root( p: integer; x, z0, epsilon: real ): real; 
var 
  i: integer;
  old, z: real;
begin
  z := z0;
  repeat
    old := z; 
    у := old;
    for  i:= 2 to p - 1 do у:= y*old;
    z := (p - l)*old/p + x/ (p*y); 
  until abs( z - old ) < epsilon;
end;

    Из теории численных методов известно, что требуемое количество n итераций для достижения заданной точности имеет порядок . Этот процесс сходится (заканчивается) очень быстро: уже при 5 итерациях достигается точность выше 10^-9.

    В общем случае условие в операторе while или в операторе repeat делит область комбинаций исходных и промежуточных данных, т.е. область возможных состояний программы на момент начала исполнения оператора цикла на две части: для первой условие выполняется, а для второй - нет. Если начальное состояние принадлежит первой подобласти (для while) или второй подобласти (для repeat), то с каждым выполнением тела цикла состояние (как точка в пространстве состояний) будет перемещаться по некоторой траектории, зависящей от операций, заданных в теле, до тех пор, пока не пересечет границу области. Именно количество шагов до пересечения границы и определяет сложность этого участка программы.

    На следующем шаге мы рассмотрим анализ сложности рекурсивных алгоритмов.

Предыдущий шаг Содержание Следующий шаг