На этом шаге мы рассмотрим задачу о k-выполнимости.

Задача о k-выполнимости - это задача о выполнимости для выражений, в которых длины дизъюнктов не превосходят величины k (рисунок 1).

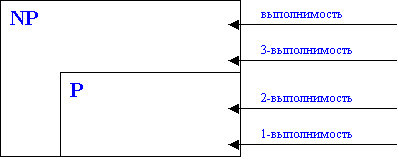
Рис.1. Задачи k-выполнимости попадают в разные классы

Разумеется задача о k-выполнимости проще задачи о (k+1)-выполнимости, и проще общей задачи о выполнимости для любого конечного k. Самая простая - задача об 1-выполнимости. В этом случае любой дизъюнкт состоит только из одной переменной или ее отрицания, т. е. Φ(x₁, x₂, ..., x_m) = & . Если все переменные в записанной конъюнкции различны, то выражение выполнимо, а если одна и та же переменная встречается два раза, в одном случае с показателем 1, а в другом случае с показателем 0, то в соответствии с известным тождеством x^l&x⁰ = 0 выражение тождественно равно нулю, т. е. не выполнимо. Проверка этого требует времени, линейного по отношению к длине выражения.

Вывод: задача об 1-выполнимости принадлежит классу Р.

Прежде, чем рассматривать задачу о 2-выполнимости, опишем мощное и очень интересное средство получения новых результатов, используемое в математической логике и в системах искусственного интеллекта. Это принцип резолюции.

Пусть у нас имеется два дизъюнкта, причем один из них содержит литерал x, а второй - литерал ¬x. Иногда эту пару литералов называют контрарной. Пример таких двух дизъюнктов приведен ниже:

Из этих двух дизъюнктов можно образовать один новый, выбросив контрарную пару, знак & и лишние скобки. В нашем примере получится дизъюнкт . Построенный дизъюнкт называется резольвентой.

В математической логике известна простая теорема: резольвента D полученная из двух дизъюнктов D₁ и D₂ является логическим следствием этих дизъюнктов, иначе говоря, истинна формула D₁ & D₂ → D.

Таким образом, к имеющейся КНФ всегда можно приписать резольвенту каких-либо двух дизъюнктов из этой КНФ (разумеется, приписать со знаком &). Ничего при этом, кроме вида формулы, не изменится. Если прежняя КНФ была выполнимой, то и новая останется таковой; если была невыполнимой, то и новая будет невыполнимой. Старая и новая КНФ эквивалентны. Чем же хороша новая КНФ? Ведь она длиннее. Старая содержит подвыражение D₁ & D₂ , а новая - подвыражение D₁ & D₂ & D. Для того чтобы ответить на этот вопрос, нужно внимательнее присмотреться к получающимся резольвентам.

Простейшие дизъюнкты - однолитеральные. Для однолитеральных дизъюнктов можно построить резольвенту только в том случае, если литералы образуют контрарную пару. При этом резольвента оказывается пустой! (Пример: D₁ = x, D₂ = ¬x, D = пусто). С точки зрения логики пустая резольвента соответствует значению false и, следовательно, КНФ в целом будет невыполнимой.

Это дает нам метод проверки невыполнимости КНФ. Следует строить все возможные резольвенты и присоединять их к КНФ, затем строить новые резольвенты по дизъюнктам расширенной (новой) КНФ, т. е. резольвенты резольвент, до тех пор, пока не будет получен пустой дизъюнкт. Это момент остановки. Ответ "КНФ невыполнима" получен. В этой процедуре последовательного получения резольвент и состоит принцип резолюции.

Заметим, что ответ "КНФ выполнима" этой процедурой не предусматривается, так как отсутствие пустого дизъюнкта на некотором шаге не означает, что он не будет получен на следующем шаге, а условия остановки в отсутствие пустого дизъюнкта не описаны. Тем не менее, для проверки 2-выполнимости принцип резолюции вполне подходит.

Теорема.

Задача о 2-выполнимости принадлежит классу Р.

Доказательство.

В этой задаче часть дизъюнктов может иметь длину 1 (переменные или их отрицания, не более 2n), остальные дизъюнкты D_i имеют вид

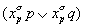, p≠q. Следовательно, максимально возможное число дизъюнктов в выражении равно 2n+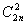- n =2n². Как бы в дальнейшем ни преобразовывали начальное выражение, число дизъюнктов в нем не будет превосходить 2n² при условии, что новый дизъюнкт не добавляется в выражение, если точно такой же дизъюнкт там уже есть. Обозначим через S множество дизъюнктов в исходной КНФ.

Рассмотрим все пары дизъюнктов в S и найдем возможные резольвенты. Это работа сложности O(|S|²) = O(n⁴). Если одна из резольвент является пустой, то прекратим выполнение алгоритма и выдадим результат: "КНФ не выполнима", иначе включим новые резольвенты (без повторов) в S; эта работа требует не более чем O(n⁴) времени.
Если в результате выполнения п.1 множество S не изменилось, то прекратим выполнение алгоритма и выдадим результат: "КНФ выполнима", иначе повторим п.1.

Пункт 1 повторяется, если на очередном шаге появляется хотя бы одна новая резольвента. Поскольку резольвента - это дизъюнкт, а их не более, чем 2n², то количество повторений п.1 ограничено величиной O(n²). Общая сложность алгоритма получается O(n⁴)*O(n²)=O(n⁶). Следовательно, 2-ВЫПОЛНИМОСТЬ является задачей полиномиальной сложности.

Необходимо отметить, что наш подход неприменим к задаче о k-выполнимости при k > 2, так как резольвенты в этом случае могут иметь длину 2(k-1), т. е. выводить преобразованную формулу за условия задачи. В общей задаче о выполнимости резольвенты не нарушают ограничения, но количество возможных дизъюнктов растет как сумма биномиальных коэффициентов , поэтому сложность п.1 и количество его повторений в данном алгоритме становятся экспоненциальными.

Не только наш подход, но и многие другие неприменимы к задаче о k-выполнимости, начиная с k=3. Различие между случаями k = 2 и k = 3 настолько значительно, что 3-ВЫПОЛНИМОСТЬ вместе с общей задачей о ВЫПОЛНИМОСТИ попадают в класс NP-полных задач, т. е. самых сложных в классе NP и, если NP ≠ P, то эти задачи не полиномиальной сложности.

Интуитивно ясно, что с увеличением k сложность задачи растет, но оказывается, что, начиная с k=3, относительное увеличение сложности задачи по отношению к общей сложности невелико. Известен в какой-то мере удивительный факт: если у нас есть алгоритм, решающий задачу о k-выполнимости, то можно с его помощью и небольшими дополнительными затратами решить общую задачу о ВЫПОЛНИМОСТИ.

На следующем шаге мы рассмотрим теорему о полиномиальной сводимости задачи ВЫПОЛНИМОСТЬ к задаче 3-ВЫПОЛНИМОСТЬ.

Предыдущий шаг Содержание Следующий шаг