Шаг 10.
Сложность задачи. Теорема о полиномиальной сводимости задачи ВЫПОЛНИМОСТЬ к задаче 3-ВЫПОЛНИМОСТЬ

    На этом шаге мы рассмотрим теорему о полиномиальной сводимости задачи ВЫПОЛНИМОСТЬ к задаче 3-ВЫПОЛНИМОСТЬ.

Теорема.

Задача ВЫПОЛНИМОСТЬ полиномиально сводима к задаче 3-ВЫПОЛНИМОСТЬ.

Доказательство.

Пусть имеется КНФ общего вида (без априорного ограничения на длину дизъюнктов). Для доказательства теоремы нам требуется построить КНФ₃, в которой длины дизъюнктов ограничены величиной три, такую, что КНФ выполнима тогда и только тогда, когда выполнима КНФ₃. Не нужно путать одновременную выполнимость двух формул с эквивалентностью (в логическом смысле) этих формул. Более того, эти формулы будут иметь даже различное число переменных.

    КНФ выполнима, если существует набор α₁, α₂, ..., α_n значений переменных x₁, x₂, ..., x_n такой, что каждый дизъюнкт обращается в единицу. Рассмотрим произвольный дизъюнкт (z₁∨ z₂ ∨ ...∨ z_k), k > 3, из исходной КНФ. Здесь z_i - литералы, т. е. переменные x_j или их отрицания.

    Сначала обсудим частный случай, k=4, дизъюнкт D = (z₁∨ z₂ ∨ z₃∨ z₄). Введем дополнительную переменную y и построим конъюнкцию двух дизъюнктов D1& D2 = (z₁∨ z₂ ∨ y)&(¬y ∨ z₃ ∨ z₄). Обратим внимание на то, что дизъюнкт D является резольвентой вновь введенных дизъюнктов D₁ и D₂ , т. е. является их следствием. Если исходная формула (конъюнкция дизъюнктов) выполнима, то при подстановке констант в D = (z₁∨ z₂ ∨ z₃∨ z₄) хотя бы один из литералов принимает значение 1. Пусть это литерал z₁. Тогда найдется такая константа γ, что подставив ее вместо y, обеспечим равенство 1 обоих дизъюнктов, D₁ и D₂. В данном случае γ = 0.

    Пусть какой-то набор из 5 констант а₁, а₂, а₃, а₄, γ доставляет значение 1 дизъюнктам D₁ и D₂. Невозможно, чтобы в этом наборе только константа γ была равна единице (иначе какой-то из двух дизъюнктов будет равен 0). Следовательно, как минимум одна из констант а₁, а₂, а₃, а₄, должна быть равна единице и дизъюнкт D при этой подстановке равен единице.

    Теперь перейдем к общему случаю. Дизъюнкту (z₁∨ z₂ ∨ z₃∨ z₄) длины k из КНФ общего вида поставим в соответствие логическое произведение дизъюнктов длины 3:

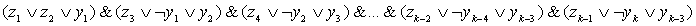
    Здесь введены новые (вспомогательные) переменные у₁,y₂, ..., y_k-3.

    Предположим, что КНФ выполнима. Тогда существует такой набор констант, подставляемых вместо переменных x₁, x₂, ..., x_n что все дизъюнкты КНФ, в том числе и дизъюнкт (z₁∨ z₂ ∨ z₃∨ z₄) равны единице. Это значит, что хотя бы один из литералов z_i равен единице при такой подстановке. Нам нужно теперь показать, что мы всегда можем назначить вспомогательным переменным такие значения, что записанное выше логическое произведение дизъюнктов длины 3 примет значение единицы.

    Действительно, пусть ненулевой литерал имеет номер i. Положим y_j = 1 при j <= i-2 и у_j=0 при j <= i-1. Получаем (z₁ ∨ z₂ ∨ 1)& (z₃ ∨ 0 ∨ 1)& (z₄ ∨ 0 ∨ 1)& ... &(z_i ∨ 0 ∨ 0)& (z_i+1 ∨ 1 ∨ 0)& ... &(z_k-2 ∨ 1 ∨ 0)& (z_k-1 ∨ z_k ∨ 1) = 1. Отсюда следует выполнимость КНФ₃.

    Обратно, предположим, что КНФ₃ выполнима. Тогда существует такой набор констант, подставляемых вместо переменных x₁, x₂, ..., x_n, y₁, y₂, ..., y_k-3, ..., что все дизъюнкты КНФ₃, в том числе и дизъюнкты (z₁ ∨ z₂ ∨ у₁), (z₃ ∨ ¬y₁ ∨ у₂), (z₄ ∨ ¬y₂ ∨ у₃), ..., (z_k-2 ∨ ¬y_k-4 ∨ у_k-3), (z_k-1 ∨ z_k ∨ ¬у_k-3) равны единице. Этот набор непременно должен быть таким, чтобы хотя бы один из литералов z_i был равен единице. В самом деле, если все z_i равны 0, то из (z₁ ∨ z₂ ∨ у₁), (z₃ ∨ ¬y₁ ∨ у₂), (z₄ ∨ ¬y₂ ∨ у₃), ..., (z_k-2 ∨ ¬y_k-4 ∨ у_k-3), (z_k-1 ∨ z_k ∨ ¬у_k-3) получаем (у₁) & (¬y₁ ∨ у₂) & (¬y₂ ∨ у₃) & ... & (¬y_k-4 ∨ у_k-3) & (¬y_k-3) и, последовательно раскрывая скобки слева направо и исключая нулевые произведения вида y₁ & ¬y1, y₁ & ¬y₂ & ¬y₂, y₁ & ¬y₂ & ... & y₃ & ... & y_k-3 & ¬y_k-3 получим в результате 0, что противоречит условию равенства значения КНФ₃ на выбранном наборе.

    Поскольку хотя бы один из литералов z_i равен единице, то значение дизъюнкта (z₁ ∨ z₂ ∨ ... ∨ z_k) равно единице. Так как речь шла о произвольном дизъюнкте из КНФ, то для выполнимой КНФ₃ найдется такой набор констант, подставляемых вместо основных и вспомогательных переменных, что все дизъюнкты КНФ получат значение единицы, т.е. КНФ является выполнимой.

    Хотя длина построенной КНФ₃ превышает длину КНФ, это превышение ограничивается постоянным множителем и, следовательно, задача ВЫПОЛНИМОСТЬ полиномиально сводима к задаче 3-ВЫПОЛНИМОСТЬ.

    Доказательство завершено.

    Схема доказательства будет следующей. Поскольку нам нужно показать, что любая задача из класса NP полиномиально сводима к задаче ВЫПОЛНИМОСТЬ, то нужно:

• описать некоторый недетерминированный вычислитель, например, недетерминированную машину Тьюринга;
• поскольку задача должна решаться некоторым алгоритмом - программой недетерминированного вычислителя, нужно описать основные характеристики этой программы, в частности, требующееся для решения задачи количество элементарных шагов;
• индивидуальная задача отличается от общей задачи тем, что некоторым образом описаны конкретные входные данные; естественно способ описания данных назвать языком. Тогда сложность конкретных входных данных можно определить как длину соответствующей цепочки символов этого языка.

    И, наконец, самое главное:

• описать условия работы недетерминированного вычислителя для данного входа и условия завершения работы в виде некоторого логического выражения так, что успешное нахождение решения задачи соответствует истинному значению этого выражения.

    Тем самым поставим в соответствие произвольной задаче из NP задачу ВЫПОЛНИМОСТЬ для КНФ, порожденной этой задачей, и теорема будет доказана.

    Введем необходимые конструкции.

    Описание индивидуальной задачи. Исходные данные индивидуальной задачи описываются некоторым словом X в алфавите недетерминированной машины Тьюринга. Это слово строится по некоторым, специфическим для данной индивидуальной задачи правилам. Сложность исходных данных естественно определить как длину |X| слова X.

    Недетерминированная машина Тьюринга (НДМТ). Дополним обычную одноленточную машину Тьюринга блоком угадывания, имеющим головку (только для записи на ленту). Работа такой машины состоит из двух этапов:

• работа блока угадывания, записывающего на ленту догадку - предлагаемое решение; в результате на ленте окажется запись X$c(X), где X - слово, описывающее входные данные индивидуальной задачи; c(X) - догадка; здесь $ - разделитель;
• проверка того, действительно ли для догадки имеет место ответ "да".

    Первый этап - совершенно неалгоритмический и не будем обсуждать какие-либо его детали, кроме одной. Поскольку интересуемся задачами класса NP, то можно сказать, что длина слова c(X) должна быть ограничена полиномом относительно длины |Х| слова X. В противном случае не только проверка, а даже само чтение этого слова требовало бы экспоненциального времени.

    Второй этап - работа обычной (детерминированной) машины Тьюринга. Ее входом является слово Х$c(X), записанное на ленте, работает она по программе, переходя из состояния в состояние, читая символы с ленты и записывая символы на ленту.

Теорема.

ВЫПОЛНИМОСТЬ является NP-полной задачей.

Доказательство.

Поскольку выше уже было доказано, что ВЫПОЛНИМОСТЬ ∈ NP, то нам осталось доказать, что "Если R ∈ NP, то R сводится к задаче ВЫПОЛНИМОСТЬ за полиномиальное время".

    Рассмотрим некоторый алгоритм α, решающий задачу R на недетерминированной машине Тьюринга, и опишем условия его исполнения машиной.

    Входом алгоритма α является строка X$c(Х), ее длина равна полиному p(|Х|).

    Введем булевы (логические) переменные для описания процесса работы машины Тьюринга:

    state_k(t) - в момент времени машина находится в состоянии q_k. Эта группа переменных отслеживает изменение состояний машины. Если в начальный (нулевой) момент времени машина находится в состоянии q_x, то state₁(0)=1; все остальные переменные этой группы, связанные с моментом t = 0, равны нулю: state₂(0)=0, state₃(0)=0, ... . Поскольку R ∈ NP, то индекс t изменяется от нуля до величины, ограниченной полиномом от сложности исходных данных, 0<=t<=p(n). Индекс k ограничен константой r, так как программа машины Тьюринга имеет конечное число состояний.

    cell_j(t) - в момент времени t читающая и пишущая головка машины просматривает ячейку ленты с номером j. Индекс ограничен тем же полиномом p(n), точнее: p(n) <= j <= p(n) +1. Это ограничение определяется тем, что за единицу времени головка может сдвинуться не более, чем на одну ячейку вправо или влево, а общее время ограничено полиномом p(n).

    symbol_j(t) - в момент времени t в ячейке с номером y записан символ алфавита, имеющий номер l. Индекс l ограничен константой ν, так как алфавит конечен.

    С помощью введенных переменных необходимо сформулировать следующие шесть условий:

1. в любой момент времени машина находится точно в одном состоянии;
2. в любой момент времени головка просматривает точно одну ячейку ленты;
3. в любой момент времени каждая ячейка содержит точно один символ;
4. в момент времени t=0 вычисление находится в исходной конфигурации (исходное состояние машины и ленты);
5. не позднее, чем через p(n) шагов машина переходит в заключительное состояние (обозначаемое q_yes) и, следовательно, принимает входное слово, решив задачу распознавания;
6. для любого момента времени новая конфигурация (новое состояние машины и ленты) получается из текущей конфигурации в результате выполнения одной команды, определяемой текущей конфигурацией (текущим состоянием и читаемым символом).

    Поскольку все перечисленные условия должны выполняться, то общее условие можно записать в виде:

F(X) = G₁(X) & G₂(X) & G₃(X) & G₄(X) & G₅(X) & G₆(X),

где G_i(X) - формулы, задающие перечисленные выше условия. Выпишем теперь формулы G_i(X).

    В каком-нибудь состоянии машина должна находиться в любой момент времени:

stale₁(t) ∨ state₂(t) ∨ state₃(t) ∨ ... ∨ state_r(t), 0 <= t <= p(n),

но не в двух сразу:

¬(state_i(t) & state_j(t)) = ¬state_i(t) ∨ ¬state_j(t), 0 <= t <= p(n), 1 <= i < j <= r.

    Таким образом,

G₁ = (&_t ∨_k state_k(t)) & (&_t,i,j (¬state_i(t) ∨ ¬state_j(t)).

    Здесь &_t - конъюнкция по всем возможным значениям t, ∨_k - дизъюнкция по всем возможным значениям k. Аналогично получаются выражения для G₂ и G₃.

    G₂(X):

    G₂ = (&_t ∨_k cell_k(t)) & (&_t,i,j (¬cell_i(t) ∨ ¬cell_j(t)).

    G₃(X):

    G₃ = (&_t,j ∨_t symbol_j,k(t)) & (&_t,j,i,m (¬symbol_j,t(t) ∨ ¬cell_j,m(t)).

    G₄(X):

    В момент времени 0 машина находится в состоянии q₁: state₁(0); в этот же момент времени головка читает ячейку ленты с номером 1: сеll₁(0); в ячейках ленты с номерами 1, 2, 3, ... записано слово X$c(X), состоящее из символов s_l1, s_l2, s_l3, ..., s_lm, где l1,l2, l3, ..., lm - номера символов в алфавите, m - длина слова: symbol_1l1(0) & symbol_1l2(0) & symbol_1l3(0) & ... & symbol_mlm(0). Общая формула:

G₄(0)= state₁(0) & cell₁(0) & symbol_1,l1(0) & symbol_2,l2(0) & symbol_3,l3(0) & ... & symbol_m,lm(0).

    G5(X):

    Если считать, что q_yes имеет номер 2, q_yes= q2, то

G₅ = state₂(p(n)).

    G6(X):

    В любой момент времени t ячейка ленты с номером j не изменяется, если она не находится напротив головки:

¬symbol_j,l(t) ∨ cell_j(t) ∨ symbol_j,l(t+l).

    Изменение конфигурации машины Тьюринга происходит по команде s_l, q_k, s_l, q_k, D. Соответствующие условия для всех моментов времени, всех состояний, всех читаемых символов и всех номеров ячеек ленты может быть выражено в виде:

(¬symbol_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ cell_j+D(t+1)) & (¬symbol_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨
cell_k(t+1)) & (¬symbol_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ cell_j,l(t+1))

где D = ±1 или 0 (R, L или S - в традиционных для машин Тьюринга обозначениях) - величина шага перемещения по ленте.

    Таким образом:

    G₆ = &_t,j,l(¬symbol_j,l(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ cell_j,l(t+1)) &_t,j,l,k (¬state_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ cell_j+D(t+1)) & (¬state_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ state_k(t+1)) & (¬state_k(t) ∨ ¬cell_j(t) ∨ ¬symbol_j,l(t) ∨ symbol_j,l(t+1)).

    Таким образом, показано, как построить КНФ, соответствующую программе недетерминированной машины Тьюринга для любой задачи R ∈ NP. Заметим, что по построению длина формулы ограничена полиномом от n - длины входного слова, следовательно, R сводится к задаче ВЫПОЛНИМОСТЬ за полиномиальное время. Это приводит нас к утверждению теоремы: ВЫПОЛНИМОСТЬ является NP-полной задачей.

    На следующем шаге мы рассмотрим классы сложности NPI, NPC.

Предыдущий шаг Содержание Следующий шаг