На этом шаге мы рассмотрим алгоритм нахождения пути между вершинами.
Оба вида обхода графа - в глубину и в ширину могут быть использованы для нахождения пути (цепи) между фиксированными вершинами u и v [1, с.92]. Достаточно начать обход графа с вершины v и вести его до момента посещения вершины u.
Преимуществом обхода графа в глубину является тот факт, что в момент посещения вершины u стек содержит последовательность вершин, определяющую путь (цепь) из v в u. Это становится очевидным, если отметить, что каждая вершина, помещаемая в стек, является смежной вершиной верхнего элемента стека.
Однако недостатком использования алгоритма обхода графа в глубину для поиска пути между данными вершинами является то, что полученный таким образом путь в общем случае не будет кратчайшим путем (кратчайшей цепью).
Пример 1. Поиск пути между двумя заданными вершинами в графе с использованием обхода графа в глубину. Граф представлен структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; //Описание типа узла стека. typedef Tref TipElement; typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; } St; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void SearchGraph (int, Lref *); void W_S (svqz *, TipElement); void YDALENIE (svqz *, TipElement *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Path_Depth_First_Search (int, int); }; void main () { Spisok A; int B,E; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Определение пути между двумя заданными вершинами графа. t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } cout << "Введите начальную вершину пути: "; cin >> B; cout << "Введите конечную вершину пути : "; cin >> E; cout << "Искомый путь: "; A.Path_Depth_First_Search (B,E); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::W_S (svqz *stk, TipElement el) //Помещение элемента el в стек stk. { svqz q=new (St); (*q).Element = el; (*q).Sled = *stk; *stk = q; } void Spisok::YDALENIE (svqz *stk, TipElement *klad) //Удаление звена из стека, заданного указателем *stk. //Значение информационного поля удаляемого звена сохраня- //ется в параметре klad. { svqz q; if (*stk==NULL) cout<<"Попытка выбора из пустого стека!\n"; else { *klad = (**stk).Element; q = *stk; *stk = (**stk).Sled; delete q; } } void Spisok::Path_Depth_First_Search (int B, int E) //Путь между вершинами B и E в графе, заданном указателем Head. { Lref s,r; Tref t; svqz UkZv; //Рабочий указатель для перемещения по стеку. svqz Stack = NULL; //Стек пуст. //Определим указатель на вершину B s = Head; while (s!=Tail) { if (s->Key==B) r = s; s = s->Next; } //Посетим первую непосещенную вершину графа и //поместим ее в первоначально пустой стек. if (r->Key==E) goto Metka; r->Flag = FALSE; W_S (&Stack,r->Trail); while (Stack!=NULL) { //Рассмотрим "верхушку" стека. t = Stack->Element; if (t->Id->Trail!=NULL) //У рассматриваемой вершины есть смежные вершины. { if (t->Id->Flag) //У рассматриваемой вершины есть //непосещенные смежные вершины. { //Посетим рассматриваемую вершину //и поместим указатель на ее список смежности в стек. if (t->Id->Key==E) goto Metka; t->Id->Flag = FALSE; W_S (&Stack,t->Id->Trail); } //У рассматриваемой вершины нет //непосещенных смежных вершин. else { t = Stack->Element; if (t->Next!=NULL) //Заменяем верхушку стека указателем //на следующий элемент списка смежности... { YDALENIE (&Stack,&t); W_S (&Stack,t->Next); } //или удаляем верхушку стека. else YDALENIE (&Stack,&t); } } //У рассматриваемой вершины нет смежных вершин. else { if (t->Id->Flag) //Посетим рассматриваемую вершину. { if (t->Id->Key==E) goto Metka; t->Id->Flag = FALSE; } t = Stack->Element; if (t->Next!=NULL) //Заменяем верхушку стека указателем //на следующий элемент списка смежности... { YDALENIE (&Stack,&t); W_S (&Stack,t->Next); } //или удаляем верхушку стека. else YDALENIE (&Stack,&t); } } Metka: UkZv = Stack; while ( UkZv!=NULL ) { cout << UkZv->Element->Id->Key << " "; UkZv = UkZv->Sled; } cout << B << endl; }
Для ориентированного графа, представленного на рисунке 1:
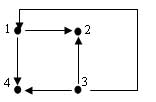
Рис.1. Пример графа
результат работы программы изображен на рисунке 2. Обратите внимание, что найден не оптимальный путь!
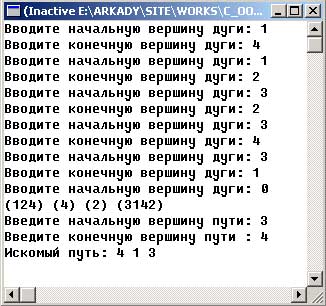
Рис.2. Результат работы приложения
Использование алгоритма обхода графа в ширину позволяет получить кратчайший путь между двумя фиксированными вершинами [1, с.93].
Пример 2. Поиск пути между двумя заданными вершинами в графе с использованием обхода графа в ширину (нерекурсивный алгоритм). Граф представлен структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct Leader *Lref; // Тип: указатель на заголовочный узел. typedef struct Trailer *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct Leader { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. }; //Описание типа дугового узла. typedef struct Trailer { Lref Id; Tref Next; }; //Описание типа узла очереди. typedef Lref TipElement; //Указатель на звено заголовочного списка. typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; }; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void Udalenie_A (svqz *, svqz *, TipElement *); void Dobavlenie (svqz *, svqz *, TipElement); void SearchGraph (int, Lref *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Path_Breadth_First_Search (Lref, int, int); }; void main () { Spisok A; int B,E; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Определение пути между двумя заданными вершинами графа. t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } cout << "Введите начальную вершину пути: "; cin >> B; cout << "Введите конечную вершину пути : "; cin >> E; cout << "Искомый путь: "; A.Path_Breadth_First_Search(A.GetHead(),B,E); cout<<endl; } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<(*p).Key<<"("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Dobavlenie (svqz *L, svqz *R, TipElement elem) //Добавление элемента elem в очередь, заданную указателями L и R. { svqz K = new (Zveno); K->Element = elem; K->Sled = NULL; if (*L==NULL) { (*L) = K; (*R) = K; } else { (*R)->Sled = K; (*R) = K; } } void Spisok::Udalenie_A (svqz *L, svqz *R, TipElement *A) //Удаление элемента из очереди, заданной указателями L и R и //помещение удаленного элемента в переменную A. { svqz q; if ((*L)!=NULL) if ((*L)->Sled!=NULL) { (*A) = (*L)->Element; q = (*L); (*L) = (*L)->Sled; delete q; } else { (*A) = (*L)->Element; delete *L; (*L) = (*R) = NULL; } } void Spisok::Path_Breadth_First_Search (Lref H, int B, int E) //Путь в графе, заданном указателем H, между вершинами B и E. { svqz L; //Указатель на начало очеpеди. svqz R; //Указатель на конец очеpеди. Lref p; //Рабочий указатель. Tref t; //Рабочий указатель. int Pred[30]; //Элемент Pred[i] содержит вершину графа, //"предшествующую" данной. int i; L = R = NULL; // Построение пустой очеpеди. //Определим указатель на вершину B и поместим его в очередь. p = H; while ( p!=Tail ) { if ( p->Key==B ) { Dobavlenie (&L,&R,p); p->Flag = FALSE; } p = p->Next; } //Пока очеpедь не пуста... while (L!=NULL) { Udalenie_A (&L,&R,&p); t = p->Trail; while (t!=NULL) { if (t->Id->Flag) { Dobavlenie (&L,&R,t->Id); t->Id->Flag = FALSE; Pred [t->Id->Key] = p->Key; } t = t->Next; } } i = E; cout << E << ' '; while (i!=B) { cout << Pred[i] <<' '; i = Pred[i]; } cout << endl; }
Результат работы программы для ориентированного графа, изображенного на рисунке 1, отражен на рисунке 3:
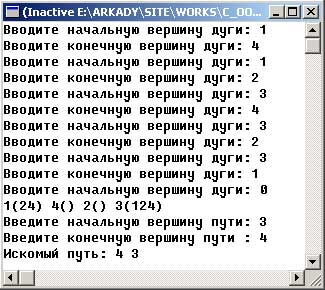
Рис.3. Результат работы приложения
Вернемся теперь к функциональному программированию.
Мы уже упоминали о том, что параметр PATH функции DEFI (смотри шаг 96) описывает путь из начальной вершины в просматриваемую. Поэтому алгоритм обхода графа в глубину можно легко модифицировать в алгоритм поиска пути между заданными вершинами (например, вершинами ROOT и END).
Пример 3.
(DEFUN TESTWAY (LAMBDA NIL
(PRINT "Построение графа.")
(SETQ GRAPH NIL) ;Инициализация
(PRINT "Введите список вершин графа:") (SETQ NODE (READ))
(PRINT "Введите список списков смежных вершин:")
(SETQ NODELIST (READ))
(PRINT (SETQ GRAPH (PAIRLIS NODE NODELIST GRAPH)))
(PRINT "Приступим к поиску пути между заданными вершинами")
(PRINT " с использованием обхода графа в глубину... ")
(PRINT "Введите начальную вершину пути:") (SETQ ROOT (READ))
(PRINT "Введите конечную вершину пути:") (SETQ END (READ))
(WAY GRAPH ROOT END)
))
; ------------------------------------
(DEFUN PAIRLIS (LAMBDA (KEY ADJ GRAPH)
; Построение графа из списка вершин KEY и списка списков
; смежных вершин ADJ путем добавления к существующему
; графу GRAPH
(COND ( (NULL KEY) GRAPH )
( (NULL ADJ) GRAPH )
( T (CONS (CONS (CAR KEY) (CAR ADJ))
(PAIRLIS (CDR KEY) (CDR ADJ) GRAPH)) )
)
))
; ---------------------------------
(DEFUN WAY (LAMBDA (GRAPH ROOT END)
; Построение пути в графе GRAPH между вершинами ROOT и END
(COND ( (NULL GRAPH) NIL )
( T (DEFI GRAPH (LIST ROOT) (LIST ROOT) END) )
)
))
; ------------------------------------------
(DEFUN DEFI (LAMBDA (GRAPH VISITED PATH END)
; GRAPH - граф, представленный структурой смежности в
; виде ассоциативного списка,
; VISITED - список уже посещенных вершин,
; PATH - список вершин, определяющий путь посещения
; END - конечная вершина пути
(COND ( (NULL PATH) (REVERSE VISITED) )
( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH)))
(DEFI GRAPH VISITED (CDR PATH) END)
)
( (EQ (EXPND GRAPH VISITED (CAR PATH)) END)
(REVERSE (CONS END PATH)) )
( T (DEFI GRAPH
(CONS (EXPND GRAPH VISITED
(CAR PATH))
VISITED)
(CONS (EXPND GRAPH VISITED
(CAR PATH))
PATH)
END) )) )
)
))
; -----------------------------------------
(DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX)
; Выбор в графе GRAPH следующей еще не просмотренной
; вершины, смежной с вершиной 2VERTEX
(COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL )
( T (FIRSTNOTVISITED
VISITED
(NEIGHBOUR3 VERTEX GRAPH))
)
)
))
; --------------------------------------------
(DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST)
; Поиск первой непосещенной вершины в списке VLIST
; VISITED - список уже посещенных вершин
(COND ( (NULL VLIST) NIL )
( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED))
(CAR VLIST)
)
( T (FIRSTNOTVISITED
VISITED
(CDR VLIST))
)
)
)
)
))
; ---------------------------------
(DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH)
; Функция возвращает список вершин графа GRAPH, смежных с
; вершиной X
(COND ( (NULL (ASSOC X GRAPH)) NIL )
( T (CDR (ASSOC X GRAPH)) )
)
))
Рассмотрим тестовые примеры для изображенного на рисунке ориентированного графа:
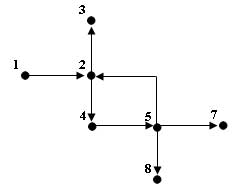
Рис.4. Пример графа
1) $ (TESTWAY)
Построение графа.
Введите список вершин графа:
(1 2 3 4 5 7 8)
Введите список списков смежных вершин:
((2) (3 4) () (5) (2 7 8) () ())
((1 2) (2 3 4) (3) (4 5) (5 2 7 8) (7) (8))
Приступим к поиску пути между заданными вершинами
с использованием обхода графа в глубину...
Введите начальную вершину пути:
1
Введите конечную вершину пути:
5
(1 2 4 5)
2) $ (TESTWAY)
Построение графа.
Введите список вершин графа:
(1 2 3 4 5 7 8)
Введите список списков смежных вершин:
((2) (3 4) () (5) (2 7 8) () ())
((1 2) (2 3 4) (3) (4 5) (5 2 7 8) (7) (8))
Приступим к поиску пути между заданными вершинами
с использованием обхода графа в глубину...
Введите начальную вершину пути:
1
Введите конечную вершину пути:
1
(1 2 3 4 5 7 8)
Обратите внимание на тот факт, что если пути из вершины ROOT в вершину END не существует, то функция (WAY GRAPH ROOT END) возвращает результат обхода графа в глубину.
(1) Липский В. Комбинаторика для программистов. - М.: Мир, 1988. - 213 с.
На следующем шаге мы познакомимся с Эйлеровыми путями и циклами.
