На этом шаге мы рассмотрим алгоритм нахождения компонент двусвязности.
- Определение [1, с.101].
- Вершину a неориентированного графа G=(V,E) будем называть
точкой сочленения, если удаление этой вершины и всех инцидентных ей ребер ведет к увеличению числа компонент связности графа.
Неориентированный граф называется двусвязным, если он связный и не содержит точек сочленения.
Произвольный максимальный двусвязный подграф графа G называется компонентой двусвязности или блоком этого графа.
Двусвязность графа - очень желательный признак для некоторых приложений. Представим себе, что вершины графа изображают узлы некоторой информационной сети, а ребра соответствуют линиям передачи. Если наш граф двусвязный, то выход из строя отдельного узла w никогда не приведет к потере соединения между любыми двумя узлами, отличными от w. Знание блоков графа также очень важно, если принять во внимание то, что многие графовые задачи, такие как нахождение всех элементарных циклов или установление факта планарности графа (граф называется планарным, если его можно так начертить на плоскости, чтобы никакие два ребра не пересекались), приводят естественным путем к аналогичным задачам для блоков данного графа.
Нахождение точек сочленения и блоков графа является классической задачей, которую можно эффективно решить "погружением" в процедуру обхода графа в глубину.
Пример.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. int WGN; //Характеристика узла. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; //Описание типа узла стека. typedef Lref TipElement; typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element1; TipElement Element2; svqz Sled; } St; int L[30]; //Количество элементов в массиве L //совпадает с количеством вершин графа. int num=0; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент //в конце списка заголовочных узлов. svqz Stack; //Указатель на рабочий стек. void SearchGraph (int, Lref *); void W_S (svqz *, TipElement, TipElement); void UDALENIE (svqz *, TipElement *, TipElement *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); Stack = NULL;} Lref GetHead() { return Head; } Lref &GetHead1() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void TwoLink (Lref, Lref); }; void main () { Spisok A; Lref SuperHead;//Заглавное звено списка заголовочных узлов. Lref t; //Рабочий указатель для перемещения //по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Нахождение компонент двусвязности графа. cout << "Множество ребер всех компонент двусвязности:\n"; t = A.GetHead(); while (t!=A.GetTail()) { (*t).WGN = 0; t = (*t).Next;} //Построение заглавного звена списка заголовочных звеньев. SuperHead = new (Leader); SuperHead->Key = 0; SuperHead->Next = A.GetHead(); A.GetHead1() = SuperHead; t = A.GetHead()->Next; while (t!=A.GetTail()) { if ( t->WGN==0 ) A.TwoLink (t,A.GetHead()); t = t->Next; } } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::W_S (svqz *stk, TipElement el1, TipElement el2) //Помещение el1 и el2 в стек stk. { svqz q=new (St); (*q).Element1 = el1; (*q).Element2 = el2; (*q).Sled = *stk; *stk = q; } void Spisok::UDALENIE (svqz *stk, TipElement *klad1, TipElement *klad2) //Удаление звена из стека, заданного указателем *stk. //Значение информационного поля удаляемого звена сохраня- //ется в параметрах klad1 и klad2. { svqz q; if (*stk==NULL) cout<<"Попытка выбора из пустого стека!\n"; else { *klad1 = (**stk).Element1; *klad2 = (**stk).Element2; q = *stk; *stk = (**stk).Sled; delete q; } } void Spisok::TwoLink (Lref r, Lref p) //Поиск в глубину, начиная с вершины r->Key и полагая, //что p является указателем на отца вершины r->Key. { Tref t; Lref e1,e2; num++; r->WGN = num; L[r->Key] = r->WGN; t = r->Trail; while ( t != NULL ) { if ( t->Id->WGN==0 ) { W_S (&Stack,r,t->Id); TwoLink (t->Id,r); if ( L[r->Key] > L[t->Id->Key] ) L[r->Key] = L[t->Id->Key]; if ( L[t->Id->Key] >= r->WGN ) { //Выписать ребра компоненты двусвязности. do { UDALENIE (&Stack,&e1,&e2); cout << "(" << e1->Key << " " << e2->Key << ") "; } while (!((e1->Key==r->Key && e2->Key==t->Id->Key) || (e1->Key==t->Id->Key && e2->Key==r->Key))); cout << ";\n"; } } else if (t->Id->Key != p->Key && r->WGN > t->Id->WGN) { W_S (&Stack,r,t->Id); if ( L[r->Key] > t->Id->WGN ) L[r->Key] = t->Id->WGN; } t = t->Next; } }
Результат работы приложения изображен на рисунке 1:
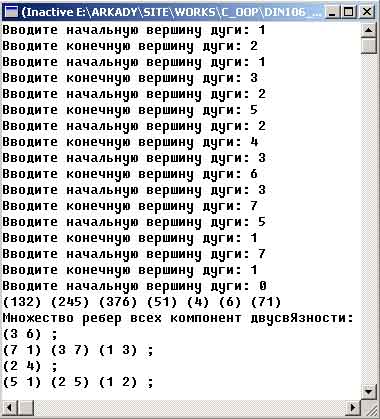
Рис.1. Результат работы приложения
(1) Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
Со следующего шага мы начнем знакомиться с остовами.
