На этом шаге мы изменим алгоритм обхода графа в ширину для вычисления конпонент связности.
С помощью изложенных в шагах 96 и 97 алгоритмов обхода графа можно ответить на некоторые вопросы относительно структуры графа. Мы рассмотрим здесь две задачи, связанные с обходом графа:
- вычисление компонент связности графа и
- построение остовного дерева связного графа.
- Определение.
- Рассмотрим некоторое семейство подграфов графа G.
Граф Hmax из этого семейства называется максимальным, если он не содержится ни в каком другом графе из рассматриваемого семейства.
Максимальный связный подграф графа G называется связной компонентой G (компонентой связности G). В связном графе имеется единственная связная компонента, совпадающая с самим графом.
Вычисление компонент связности
Отметим, что алгоритм обхода графа в глубину можно легко модифицировать так, чтобы он вычислял связные компоненты этого графа.
Пример 1. Иллюстрация использования обхода графа в глубину для нахождения всех его связных компонент. Граф представлен структурой Вирта.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Boolean Flag; //Флаг посещения узла при обходе. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; //Описание типа узла стека. typedef Tref TipElement; typedef struct Zveno *svqz; typedef struct Zveno { TipElement Element; //Указатель на список смежности. svqz Sled; } St; class Spisok { private: Lref Head; //Указатель на голову списка заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент // в конце списка заголовочных узлов. void SearchGraph (int, Lref *); public: Spisok() {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } Lref GetHead() { return Head; } Lref GetTail() { return Tail; } void MakeGraph (); void PrintGraph (); void Depth_First_Search (Lref); void LinkComp(); }; void main () { Spisok A; Lref t; //Рабочий указатель для перемещения // по списку заголовочных звеньев. //Построение графа и вывод его структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Рекурсивный обход графа в глубину. cout<<"Результат рекурсивного обхода...\n"; t = A.GetHead(); while (t!=A.GetTail()) { (*t).Flag = TRUE; t = (*t).Next; } A.Depth_First_Search (A.GetHead()); cout<<endl; //Вывод компонент связности. cout<<"Компоненты связности:\n"; A.LinkComp(); } void Spisok::SearchGraph (int w, Lref *h) //Функция возвращает указатель на заголовочный узел //с ключом w в графе, заданном структурой Вирта с указателем Head. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x, &p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::PrintGraph () //Вывод структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::Depth_First_Search (Lref r) //Рекурсивный обход графа в глубину. r - указатель //на структуру Вирта. { Tref t; t = (*r).Trail; cout<<(*r).Key; (*r).Flag = FALSE; while (t!=NULL) { if ((*(*t).Id).Flag) Depth_First_Search ((*t).Id); t = (*t).Next; } } void Spisok::LinkComp() //Определение компонент связности в графе, заданном //структурой Вирта с указателем Head. { Lref t = Head; while (t !=Tail) { t->Flag = TRUE; t = t->Next; } t = Head; while ( t!=Tail ) { if ( t->Flag ) { Depth_First_Search (t); cout << endl; } t = t->Next; } }
Результат работы приложения изображен на рисунке 1:
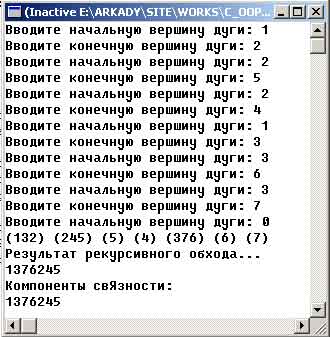
Рис.1. Результат работы приложения
Для вычисления компонент связности графа на языке LISP воспользуемся уже написанной ранее функцией DEPTHFIRST [1].
Рассмотрим еще раз работу функции DEFI. Заметим, что когда к списку просмотренных вершин VISITED добавляется новая вершина, список PATH представляет собой путь из этой вершины в начальную. Поэтому по окончанию работы в списке VISITED содержатся только те вершины, которые можно соединить с начальной. Можно показать [2], что в этом списке содержатся все вершины, обладающие этим свойством.
Таким образом, можно сказать, что функция DEPTHFIRST вычисляет список вершин связной компоненты вершины ROOT, и теперь мы готовы решить задачу о построении всех компонент связности данного графа.
Проще всего это сделать в два этапа.
1. Сначала построим списки вершин компонент связности.
Программа [3, с.129-130].
(DEFUN CONNLISTS (LAMBDA (GRAPH) ; Построение списка списков вершин компонент связности ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка (CONNLSTS GRAPH NIL) )) ; ----------------------------------- (DEFUN CONNLSTS (LAMBDA (GRAPH LISTS) (COND ( (NULL GRAPH) LISTS ) ( T (COND ( (NULL (LMEMBER (CAAR GRAPH) LISTS)) (CONNLSTS (CDR GRAPH) (CONS (DEPTHFIRST GRAPH (CAAR GRAPH)) LISTS)) ) ( T (CONNLSTS (CDR GRAPH) LISTS) )) ) ) )) ; ----------------------------------- (DEFUN LMEMBER (LAMBDA (VERTEX LISTS) ; Функция проверяет, содержится ли вершина VERTEX в ; каком-либо из списков, составляющих LISTS (AND LISTS (OR (MEMBER VERTEX (CAR LISTS)) (LMEMBER VERTEX (CDR LISTS)))) )) ; ------------------------------------ (DEFUN DEPTHFIRST (LAMBDA (GRAPH ROOT) ; Обход графа в глубину: ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; ROOT - вершина, с которой начинается обход графа, ; Результат: список вершин графа в порядке посещения в глубину (COND ( (NULL GRAPH) NIL ) ( T (DEFI GRAPH (LIST ROOT) (LIST ROOT)) )) )) ; -------------------------------------- (DEFUN DEFI (LAMBDA (GRAPH VISITED PATH) ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; VISITED - список уже посещенных вершин, ; PATH - список вершин, определяющий путь посещения (COND ( (NULL PATH) (REVERSE VISITED) ) ( T (COND ( (NULL (EXPND GRAPH VISITED (CAR PATH))) (DEFI GRAPH VISITED (CDR PATH)) ) ( T (DEFI GRAPH (CONS (EXPND GRAPH VISITED (CAR PATH)) VISITED) (CONS (EXPND GRAPH VISITED (CAR PATH)) PATH)) )) ) ) )) ; ----------------------------------------- (DEFUN EXPND (LAMBDA (GRAPH VISITED VERTEX) ; Выбор в графе GRAPH следующей еще не просмотренной ; вершины, смежной с вершиной VERTEX (COND ( (NULL (NEIGHBOUR3 VERTEX GRAPH)) NIL ) ( T (FIRSTNOTVISITED VISITED (NEIGHBOUR3 VERTEX GRAPH)) ) ) )) ; -------------------------------------------- (DEFUN FIRSTNOTVISITED (LAMBDA (VISITED VLIST) ; Поиск первой непосещенной вершины в списке VLIST ; VISITED - список уже посещенных вершин (COND ( (NULL VLIST) NIL ) ( T (COND ( (NULL (MEMBER (CAR VLIST) VISITED)) (CAR VLIST) ) ( T (FIRSTNOTVISITED VISITED (CDR VLIST)) )) ) ) )) ; --------------------------------- (DEFUN NEIGHBOUR3 (LAMBDA (X GRAPH) ; Функция возвращает список вершин графа GRAPH, смежных с ; вершиной X (COND ( (NULL (ASSOC X GRAPH)) NIL ) ( T (CDR (ASSOC X GRAPH)) )) ))
Тестовые примеры:
$ (CONNLISTS '((1 . (2 3)) (2 . (3)) (5 . ()))) ((5) (1 2 3)) $ (CONNLISTS '((1 . (2 3)) (2 . (3)) (5 . ()) (6 . ()))) ((6) (5) (1 2 3)) $ (CONNLISTS '((1 . (2 3)) (2 . (3)) (5 . (6)))) ((5 6) (1 2 3)) $ (CONNLISTS '((1 . (2 3 5)) (2 . (3)) (5 . (6)))) ((1 2 3 5 6))
2. Теперь не составляет труда написать функцию, возвращающую структуры смежности, соответствующие компонентам связности. Для этого мы воспользуемся следующими вспомогательными функциями:
(DEFUN F2 (LAMBDA (GRAPH LST) ; Построение структур смежности всех компонент связности ; GRAPH - граф, представленный структурой смежности в ; виде ассоциативного списка, ; LST - список списков компонент связности (COND ( (NULL LST) NIL ) ( T (CONS (F1 GRAPH (CAR LST)) (F2 GRAPH (CDR LST))) )) )) ; --------------------------- (DEFUN F1 (LAMBDA (GRAPH LST) (COND ( (NULL GRAPH) NIL ) ( (MEMBER (CAAR GRAPH) LST) (CONS (CAR GRAPH) (F1 (CDR GRAPH) LST)) ) ( T (F1 (CDR GRAPH) LST) )) ))
Тестовый пример:
$ (F2 '((1 . (2 3)) (4 . (5 6)) (5 . (4)) (3 . (2 1))) '((1 2 3) (4 5 6))) (((1 2 3) (3 2 1)) ((4 5 6) (5 4)))
(1) Крюков А.П., Радионов А.Я., Таранов А.Ю., Шаблыгин Е.М. Программирование на языке R-Лисп. - М.: Радио и связь, 1991. - 192 с.
(2) Баррон Д. Рекурсивные методы в программировании. - М.: Мир, 1974. - 80 с.
(3) Turbo Pascal Version 3.0 Reference Manual. Borland International, 1985.
На следующем шаге мы рассмотрим нахождение компонент двусвязности.
