На этом шаге мы рассмотрим эти преобразования на проскости.
Аффинные преобразования объектов на плоскости описываются так:
X = Ах + By + С, Y = Dx + Еу + F,
Рассмотрим частные случаи аффинного преобразования.
1. Сдвиг (рисунок 1).
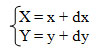
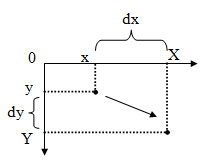
Рис.1. Сдвиг
В матричной форме:
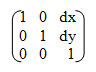
Обратное преобразование позволяет рассчитать старые координаты точек объектов по известным новым координатам:
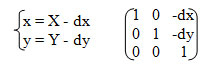
2. Растяжение-сжатие (рисунок 2).
Необходимо отметить, что это, вероятно, не очень удачное название, так как для некоторых типов объектов размеры и форма не изменяются - например, для точечных объектов. По-другому это преобразование можно назвать масштабированием.
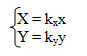
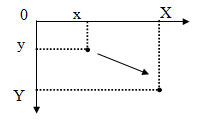
Рис.2. Растяжение/сжатие
В матричной форме:
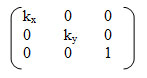
Обратное преобразование:
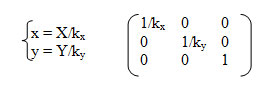
3. Поворот вокруг центра координат (0, 0) (рисунок 3).
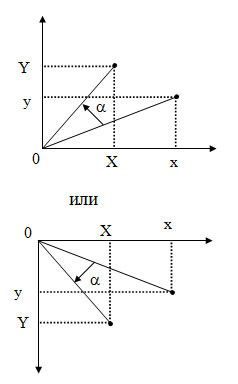
Рис.3. Поворот объекта
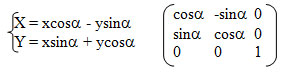
Формулы для обратного преобразования можно получить, если представить себе поворот точки с координатами (X, Y) на угол (-α):
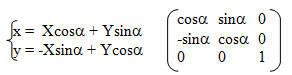
На следующем шаге мы рассмотрим аффинные преобразования в пространстве.
