На этом шаге мы рассмотрим особенности этой проекции.
Перспективную проекцию (рисунок 1) сначала рассмотрим при вертикальном расположении камеры, когда α = β = 0.
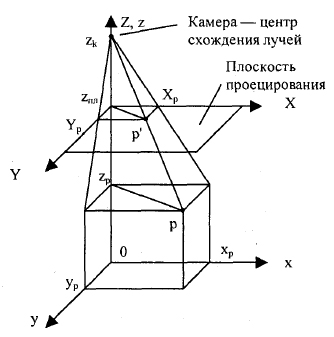
Рис.1. Перспективная проекция
Такую проекцию можно себе представить как изображение на стекле, через которое смотрит наблюдатель, расположенный сверху в точке (х, у, z) = (0, 0, zk). Здесь плоскость проецирования параллельна плоскости (x 0 y).
Исходя из подобия треугольников, запишем такие пропорции:
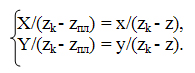
Учитывая также координату Z:
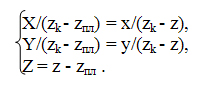
В матричной форме преобразования координат можно записать так:
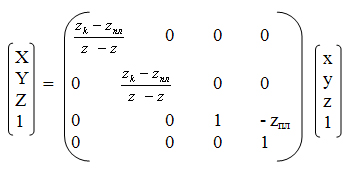
Обратите внимание на то, что здесь коэффициенты матрицы зависят от координаты z (в знаменателе дробей). Это означает, что преобразование координат является нелинейным (а точнее, дробно-линейным), оно относится к классу проективных преобразований.
Теперь рассмотрим общий случай - для произвольных углов наклона камеры (α и β) так же, как и для параллельной аксонометрической проекции. Пусть (x', у', z') - координаты для системы координат, повернутой относительно начальной системы (х, у, z) на углы α и β.
Тогда:
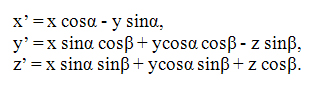
Запишем преобразования координат перспективной проекции в виде:
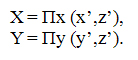
Последовательность преобразования координат можно описать так:
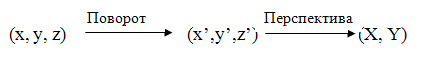
Преобразование в целом нелинейное. Его нельзя описать одной матрицей коэффициентов-констант для всех объектов сцены (хотя для преобразования координат можно использовать и матричную форму).
Для такой перспективной проекции плоскость проецирования перпендикулярна лучу, исходящему из центра (x, у, z) = (0, 0, 0) и наклоненному под углом α, β. Если камеру отдалять от центра координат, то центральная проекция видоизменяется. Когда камера в бесконечности, центральная проекция вырождается в параллельную проекцию.
На следующем шаге мы закончим изучение этого вопроса.
