На этом шаге мы рассмотрим свойства этой проекции.
Укажем основные свойства перспективного преобразования. В центральной проекции:
- не сохраняется отношение длин и площадей;
- прямые линии изображаются прямыми линиями;
- параллельные прямые изображаются сходящимися в одной точке.
Последнее свойство широко используется в начертательной геометрии для ручного рисования на бумаге. Проиллюстрируем это на примере каркаса домика (рисунок 1).
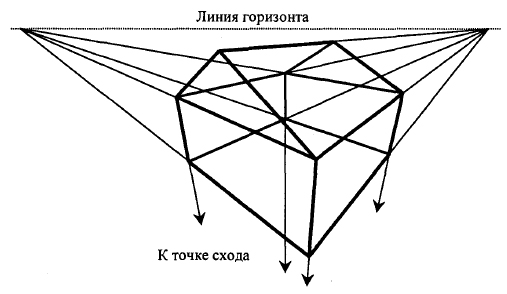
Рис.1. Параллельные линии изображаются в центральной проекции сходящимися в одной точке
Существуют и другие перспективные проекции, которые различаются положением плоскости проецирования и местом точки схождения лучей проецирования. Кроме того, проецирование может осуществляться не на плоскость, а, например, на сферическую или цилиндрическую поверхность.
Рассмотрим косоугольную проекцию, для которой лучи проецирования не перпендикулярны плоскости проецирования. Основная идея такой проекции - камера поднята на высоту h с сохранением вертикального положения плоскости проектирования (рисунок 2).
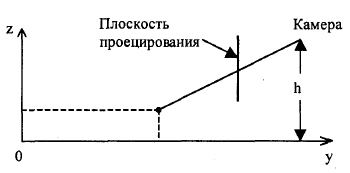
Рис.2. Косоугольная проекция
Получить такую проекцию можно следующим способом:
- Выполняем поворот вокруг оси z на угол α.
- Заменяем z' на -у', а у' на z'.
- Выполняем сдвиг системы координат вверх на высоту камеры h.
- В плоскости (х', у', 0) строим перспективную проекцию уже рассмотренным выше способом (точка схода лучей на оси z).
Преобразование координат может быть описано таким образом. Сначала определяются (х', у', z').

А потом выполняется перспективное преобразование:
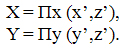
Преимущество такой проекции заключается в сохранении параллельности вертикальных линий, что иногда полезно при изображении домов в архитектурных компьютерных системах.
На следующем шаге мы рассмотрим примеры изображений в различных проекциях.
