На этом шаге мы рассмотрим особенности отображения в окне.
Как мы уже рассмотрели на предыдущих шагах, отображение на плоскость проецирования соответствует некоторому преобразованию координат. Это преобразование координат различно для разных типов проекции, но, так или иначе, осуществляется переход к новой системе координат - координатам проецирования.
Координаты проецирования могут быть использованы для формирования изображения с помощью устройства графического вывода. Однако при этом могут понадобиться дополнительные преобразования, поскольку система координат в плоскости проецирования может не совпадать с системой координат устройства отображения. Например, должны отображаться объекты, измеряемые в километрах, а в растровом дисплее единицей измерения является пиксель. Как выразить километры в пикселях?
Кроме того, вы, наверное, видели, что на экране компьютера можно показывать увеличенное, уменьшенное изображение объектов, а также их перемещать. Как это делается?
Введем обозначения. Пусть (ХЭ, YЭ, ZЭ) - это экранные координаты объектов в графическом устройстве отображения. Заметим, что не следует воспринимать слово "экранные" так, будто речь идет только о дисплеях - все нижеследующее можно отнести и к любым другим устройствам, использующим декартову систему координат. Координаты проецирования обозначим здесь как (X, Y, Z).
Назовем окном прямоугольную область вывода с экранными координатами (ХЭmin, YЭmin) - (ХЭmax, YЭmax). Обычно приходится отображать в окне или всю сцену, или отдельную ее часть (рисунок 1).
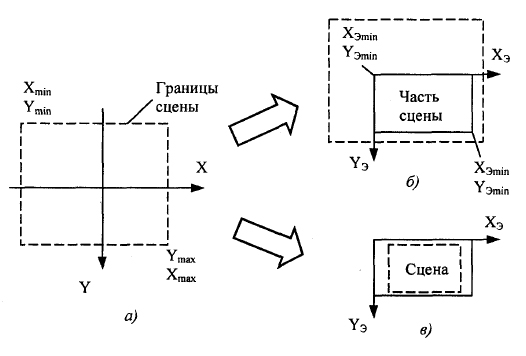
Рис.1. Отображение проекции сцены: а - границы сцены в координатах проекции; б - в окне часть сцены, в - вся сцена с сохранением пропорций вписана в окно
Преобразование координат проекции в экранные координаты можно задать как растяжение/сжатие и сдвиг:
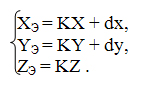
Такое преобразование сохраняет пропорции объектов благодаря одинаковому коэффициенту растяжения/сжатия (K) для всех координат. Заметим, что для плоского отображения можно отбросить координату Z.
Рассмотрим, как можно вычислить K, dx и dy. Например, необходимо вписать все изображение сцены в окно заданных размеров. Условие вписывания можно определить так:
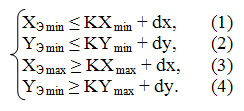
Если прибавить (1) к (3), то получим:
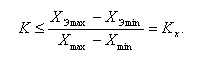
Из неравенств (2) и (4) следует:
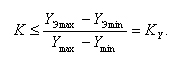
Решением системы (1)-(4) для K будет: К ≤ min {КX, KY} = Kmin.
Если значение КX или значение KY равно бесконечности, то его необходимо отбросить. Если оба - то значение Кmin можно задать равным единице. Для того чтобы изображение в окне имело наибольший размер, выберем К = Кmin. Теперь можно найти dx. Из неравенства (1):
dx ≥ XЭ min - KYmin = dx1.
Из неравенства (3):
dx ≤ XЭ max - KYmax = dx2.
Поскольку dx1 ≤ dx2, то величину dx можно выбрать из интервала dx1 ≤ dx ≤ dx2. Выберем центральное расположение в окне:
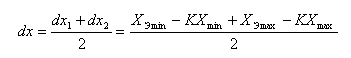
Аналогично найдем dy:
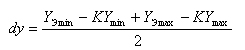
При таких значениях dx и dy центр сцены будет в центре окна.
В других случаях, когда в окне необходимо показывать с соответствующим масштабом лишь часть сцены, можно прямо задавать числовые значения масштаба (К) и координаты сдвига (dx, dy). При проектировании интерфейса графической системы желательно ограничить выбор K, dx, dy диапазоном допустимых значений.
В графических системах используются разнообразные способы задания масштаба отображения и определения границ сцены для показа в окне просмотра. Например, для сдвига часто используют ползунки скроллинга. Также можно указывать курсором точку на сцене, и затем эта точка становится центральной точкой окна. Или можно очертить прямоугольник, выделяя границы фрагмента сцены, - тогда этот фрагмент затем будет вписан в окно. И так далее. Все эти способы отображения основываются на растяжении/сжатии (масштабировании), а также сдвиге, и описываются аффинным преобразованием координат.
На следующем шаге мы подитожим сказанное.
