На этом шаге мы подитожим изложенный материал.
Представим цепочку преобразований координат от мировых к экранным следующим образом (рисунок 1):
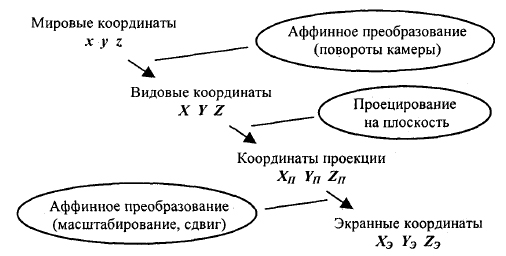
Рис.1. Этапы преобразований координат
Для аксонометрической (параллельной) проекции координаты проекции совпадают с видовыми координатами (хотя это и не обязательно). Преобразование координат можно описать одной матрицей, которая получается перемножением соответствующих матриц.
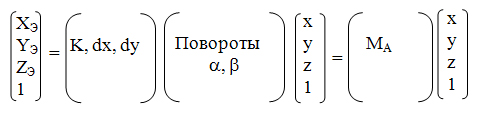
Важно то, что для аксонометрической проекции коэффициенты матрицы - это константы, одинаковые для всех точек трехмерного пространства. Это дает возможность свести к минимуму вычисления координат в цикле графического вывода. В этом плане можно отметить крайний случай, когда мировые координаты совпадают с экранными - вообще нет никаких преобразований координат. Например, координаты объектов задаются в пикселях экрана. Такое часто встречается, например, в двухмерной графике.
Для перспективной (центральной) проекции коэффициенты матрицы проецирования на плоскость не являются константами - они зависят от Z. Это делает нецелесообразным запись цепочки преобразований в виде одной матрицы и, как следствие этого, усложняется расчет координат в сравнении с параллельной проекцией.
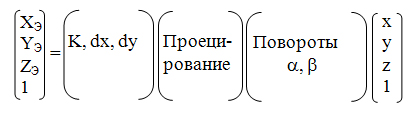
Для центральной проекции иногда используют матричную форму с применением обобщенных однородных нелинейных координат.
В качестве мировых и экранных координат нами была использована трехмерная ортогональная система. В компьютерных графических системах также используются другие системы координат и иные проекции. В особенности это касается систем, которые моделируют объекты, располагающиеся на поверхности Земли. С этими вопросами можно ознакомиться в многочисленной литературе по геодезии и картографии, а также в работах, посвященных геоинформсщионным системам.
Со следующего шага мы начнем рассматривать базовые растровые алгоритмы.
