Шаг 52.
Основы компьютерной графики.
Базовые растровые алгоритмы. Фракталы

    На этом шаге мы рассмотрим различные виды фракталов.

    Фрактал можно определить как объект довольно сложной формы, получающийся в результате выполнения простого итерационного цикла. Итерационность, рекурсивность обуславливают такие свойства фракталов, как самоподобие - отдельные части похожи по форме на весь фрактал в целом. Латинское fractus означает "составленный из фрагментов". В 1975 году французский математик Бенуа Мандельброт издал книгу "The fractal Geometry of Nature" ("Фрактальная геометрия природы"). С того времени слово "фрактал" стало модным.

    Фракталом Мандельброта названа фигура, которая порождается очень простым циклом. Для создания этого фрактала необходимо для каждой точки изображения выполнить цикл итераций согласно формуле: 

  zk+1 = zk2 + z0
где k = 0, 1, ..., n. Величины zk - это комплексные числа, zk = хk + iyk, причем стартовые значения х0 и у0 - это координаты точки изображения. Для каждой точки изображения итерации выполняются ограниченное количество раз (и) или до тех пор, пока модуль числа zk не превышает 2. Модуль комплексного числа равен корню квадратному из х2+у2. Для вычисления квадрата величины zk можно воспользоваться формулой z = (х + iy) (х + iy) = = (х2 - у2) + i(2у), поскольку i2 = -1. Цикл итераций для фрактала Мандельброта можно выполнять в диапазон х = (от -2.2 до 1), у = (от -1.2 до 1.2). Для того чтобы получить изображение в растре, нс обходимо пересчитывать координаты этого диапазона в пиксельные.


Рис.1. Фрактал Мандельброта

    Фрактал Жулиа внешне совсем не похож на фрактал Мандельброта, однако он определяется итерационным циклом, почти полность тождественным с циклом генерации Мандельброта. Формула итераций для фрактала Жулиа такая; 

  zk+1 = zk2 + c
где с - комплексная константа. Условием завершения итераций является | zk | > 2 - так же, как для фрактала Мандельброта.

    На рисунках 2 и 3 приведены различные фракталы (множества) Жулиа (источник: https://ru.wikipedia.org/wiki/Множество_Жулиа):


Рис.2. Заполненное множество Жюлиа для отображения f(z)=z2-1. Осевая симметрия свидетельствует об отсутствии мнимой составляющей в свободном члене отображения f(z)


Рис.3. Заполненное множество Жюлиа для отображения f(z)=z2+0,28+0,0113i. Завихрения против часовой стрелки свидетельствуют о положительной мнимой составляющей в свободном члене отображения f(z)

    Рассмотрим следующий пример фрактала - фрактал Ньютона (бассейны Ньютона). Для него итерационная формула имеет такой вид: 

  zk+1 = (3zk4 + 1) / (4zk3)
где z - также комплексные числа, причем z0 = х + iy соответствует координатам точки изображения.

    Условием прекращения цикла итераций для фрактала Ньютона есть приближение значений | z4- 1| к нулю.

    Приведем несколько примеров фракталов Ньютона (источник: https://ru.wikipedia.org/wiki/Бассейны_Ньютона):


Рис.4. Бассейны Ньютона


Рис.5. Бассейны Ньютона для полинома пятой степени p(x)=x5-1. Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций

    Рассмотрим еще одну разновидность фракталов. Такие фракталы названы геометрическими, поскольку их форма может быть описана как последовательность простых геометрических операций. Например, кривая Коха (снежинка Коха) становится фракталом в результате бесконечного количества итераций, в ходе которых выполняется деление каждого отрезка прямой на три части. На рисунке 6 показаны три итерации - постепенно линия становится похожей на снежинку (источник: https://ru.wikipedia.org/wiki/Кривая_Коха):


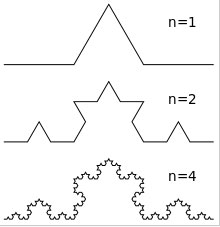
Рис.6. Кривая Коха

    Следующую группу составляют фракталы, которые генерируются согласно методу "систем итеративных функций" - IFS (Iterated Functions Systems). Этот метод может быть описан, как последовательный итеративный расчет координат новых точек в пространстве: 

  xk+1 = Fx(xk, yk),
  yk+1 = Fy(xk, yk),
где Fx и Fy - функции преобразования координат, например, аффинного преобразования. Эти функции и определяют форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов.

    Вот пример такого фрактала (источник: https://en.wikipedia.org/wiki/Iterated_function_system):


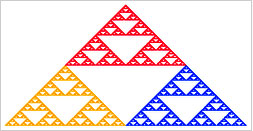
Рис.7. Ковер Серпинского

    На следующем шаге мы рассмотрим построение фрактала.




Предыдущий шаг Содержание Следующий шаг