На этом шаге мы рассмотрим алгоритм построения фрактала.

    Давайте попробуем создать фрактал, который бы выглядел как растение. Вообразим себе ствол, на котором много веточек. На каждой веточке много меньших веточек и так далее. Самые малые ветки можно считать листвой или колючками. Все элементы будем рисовать отрезками прямой. Каждый отрезок будет задаваться двумя конечными точками.

    Для начала итераций необходимо задать стартовые координаты линии. Это будут точки 1, 2. На каждом шаге итераций будем рассчитывать координаты других точек.

    Сначала находим точку 3. Это повернутая на угол α точка 2, центр поворота - в точке 1 (рисунок 1).

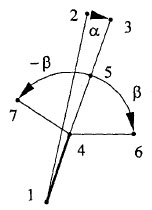
Рис.1. Опорные точки элементов фрактала

  x3 = (х2 - x1) cos α - (y2 - y1) sin α + x1, 
  y3 = (x2 - x1) sin α + (y2 - y1) cos α + y1.

    Если α = 0, то ствол и все ветви прямые. Потом на ходим точку 4. От нее будут распространяться ветви. Пусть соотношение длин отрезков 1-4 и 1-3 равно k, причем 0<k<1. Тогда для вычисления координат точки 4 можно воспользоваться следующими формулами:

  x4 = xl (1 - k) + x3 k, 
  y4 = yl (1 - k) + y3 k.

    Теперь зададим длину и угол наклона ветвей, которые выходят из точки 4. Сначала найдем координаты точки 5. Введем еще один параметр - k1, который будет определять соотношение длин отрезков 4-5 и 4-3, причем так же 0<k1<1. Координаты точки 5 равны:

  x5 = x4 (1 - k1) + x3 k1, 
  y5 = y4 (1 - k1) + y3 k1.

    Точки 6 и 7 - это точка 5, повернутая относительно точки 4 на углы β и -β соответственно:

  x6 = (x5 - x4) cos β - (y5 - y4) sin β + x4; 
  y6 = (x5 - x4) sin β + (y5 - y4) cos β + y4; 
  x7 = (x5 - x4) cos β + (y5 - y4) sin β + x4; 
  у7 = - (х5 - х4) sin β + (y5 - y4) cos β + у4.

    Кроме расчета опорных точек на каждом шаге будем рисовать один отрезок 1-4. В зависимости от номера итераций можно изменять цвет отрезка. Также можно устанавливать его толщину, например, пропорционально длине.

    Таким образом, фрактал мы задали как последовательность аффинных преобразований координат точек. Величины α, β, k, k1 - это параметры, которые описывают вид фрактала в целом. Они представляют собой константы на протяжении всего итеративного процесса. Это дает возможность в итерациях использовать только операции сложения, вычитания и умножения, если вычислить значения sin(), cos(), (1 - k) и (1 - k1) только один раз перед началом итераций как коэффициенты-константы.

    Дадим запись алгоритма в виде рекурсивной процедуры ШАГ ().

ШАГ (x1, y1, x2, y2, num)
{
  Если (xl - x2)2 + (yl - y2)2 > lmin, то
  {
  Вычисляем координаты точек 3-7:
  x3 = (x2 - x1) A - (y2 - y1) B + x1 
  y3 = (x2 - x1) B + (y2 - y1) A + y1 
  x4 = x1 C + x3 D
  y4 = y1 C + y3 D
  х5 = x4 E + x3 F
  у5 = y4 E + y3 F
  x6 = (x5 - x4) G - (y5 - y4) H + x4
  y6 = (x5 - x4) H + (y5 - y4) G	+ у4
  х7 = (x5 - x4) G + (y5 - y4) H	+ x4
  y7 = - (x5 - х4) H + (y5 - у4) G + y4
  Рисуем отрезок (x1, y1 - x4,	y4)		
  ШАГ (x4, y4, x3, y3, num)
  ШАГ (x4, y4, x6, y6, num+1)
  ШАГ (x4, y4, x7, y7, num+1)
  }			
}

    Для того чтобы нарисовать фрактал, необходимо вызывать процедуру ШАГ, установив соответствующие значения ее аргументов: ШАГ(x1, yl, x2, y2, 0) .Обратите внимание на один из аргументов этой процедуры - num, который в начале работы равен 0. В теле процедуры есть три рекурсивных вызова с различными значениями этого аргумента:

  ШАГ (x4, y4, x3, y3, num) - продолжаем ствол; 
  ШАГ (x4, y4, x6, y6, num+1) - правая ветвь; 
  ШАГ (x4, y4, x7, y7, num+1) - левая ветвь. 

    Значение num показывает степень детализации расчета дерева. Один цикл итераций содержит много шагов, соответствующих одному значению величины num. Числовое значение num можно использовать для прекращения итеративного процесса, а также для определения текущего цвета элементов "растения".

    Завершение циклов итераций в нашем алгоритме происходит тогда, когда длина ветви становится меньше некоторой величины lmin, например, lmin = 1. На рисунках 2 - 4 приведены результаты выполнения программы при значениях Этот фрактал при α = 2°, β = 86°, k = 0.14, k1 = 0.3 и значениях lmin соответственно 10, 5 и 1.

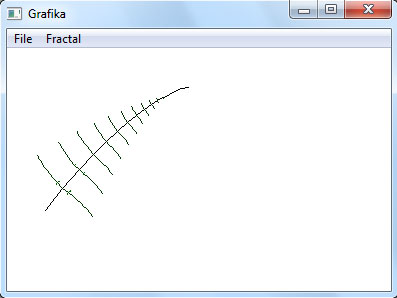
Рис.2. lmin = 10

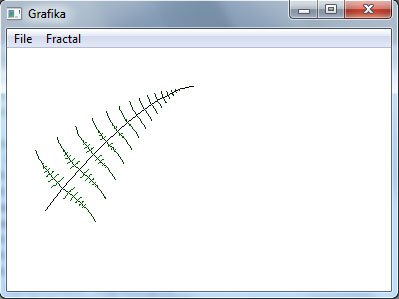
Рис.3. lmin = 5

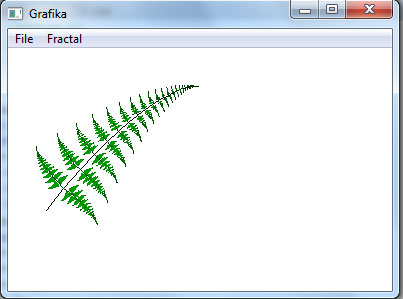
Рис.4. lmin = 1

    Приведем фрагмент программы:

.   .   .   .
// Исходные данные
int a = 2;
int b = 86;
float k = 0.14;
float k1 = 0.3;
int lmin = 1;
int MaxI = 5;
int ClrStep = 1;
// Вычисление параметров
float A = cos(a*3.14/180);
float B = sin(a*3.14/180);
float C = 1-k;
float D = k;
float E = 1 - k1;
float F = k1;
float G = cos(b*3.14/180);
float H = sin(b*3.14/180);

int Step (HDC hdc,double x1,double y1,double x2,double y2,int num);

void DrawStudyExample(HWND hWnd)
{
  HDC hdc;
  RECT rc;
  GetClientRect(hWnd,&rc);
  hdc=GetDC(hWnd);
  ClrStep=255/MaxI;

  double x1=rc.right/10,y1=2*rc.bottom/3,x2=2*rc.bottom/3,y2=0;
  Step (hdc,x1,y1,x2,y2,0);
  ReleaseDC(hWnd,hdc);
}

int Step (HDC hdc,double x1,double y1,double x2, double y2,int num)
{
  double x3,y3,x4,y4,x5,y5,x6,y6,x7,y7;
  HPEN hPenOld, hPen;

  if (sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))>lmin)
	 {
	 x3 = (x2 - x1)*A - (y2 - y1)*B + x1;
	 y3 = (x2 - x1)*B + (y2 - y1)*A + y1;
	 x4 = x1*C + x3*D;
	 y4 = y1*C + y3*D;
	 x5 = x4*E + x3*F;
	 y5 = y4*E + y3*F;
	 x6 = (x5 - x4)*G - (y5 - y4)*H + x4;
	 y6 = (x5 - x4)*H + (y5 - y4)*G + y4;
	 x7 = (x5 - x4)*G + (y5 - y4)*H + x4;
	 y7 = - (x5 - x4)*H + (y5 - y4)*G + y4;
	 hPen=CreatePen(PS_SOLID,(2*num)/3,RGB(0,ClrStep*num,0));
	 hPenOld=(HPEN)SelectObject(hdc,hPen);
	 MoveToEx(hdc,x1,y1,NULL);
	 LineTo(hdc,x4,y4);
	 SelectObject(hdc,hPenOld);
	 DeleteObject(hPen);
	 Step (hdc, x4, y4, x3, y3, num);
	 Step (hdc, x4, y4, x6, y6, num+1);
	 Step (hdc, x4, y4, x7, y7, num+1);
	 }
}

    Метод IFS применяется не только для создания изображений. Его использовали Барнсли и Слоан для эффективного сжатия графических изображений при записи в файлы. Основная идея такая: поскольку фракталы могут представлять очень сложные изображения с помощью простых итераций, то описание этих итераций требует значительно меньшего объема информации, чем соответствующие растровые изображения. Для кодирования изображений необходимо решать обратную задачу - для изображения (или его фрагмента) подобрать соответствующие коэффициенты аффинного преобразования. Этот метод используется для записи цветных фотографий в файлы со сжатием в десятки и сотни раз без заметного ухудшения изображения. Формат таких графических файлов назван FIF (Fractal Image Format) и запатентован фирмой Iterated Systems [1].

    Со следующего шага мы начнем знакомится с методами и алгоритмами трехмерной графики.

Предыдущий шаг Содержание Следующий шаг