На этом шаге мы рассмотрим первый способ представления такой модели.
Обсудим структуры данных, которые используются в векторной полигональной модели. В качестве примера объекта будет куб. Рассмотрим, как можно организовать описание такого объекта в структурах данных.
Первый способ. Сохраняем все грани в отдельности (рисунок 1).

Рис.1. Первый способ описания куба
Грань А = {(xА0, yА0, zА0), (xА1, yА1, zА1), (xА2, yА2, zА2), (xА3, yА3, zА3)}
Грань В = {(xВ0, yВ0, zВ0), (xВ1, yВ1, zВ1), (xВ2, yВ2, zВ2), (xВ3, yВ3, zВ3)}
Грань С = {(xС0, yC0, zC0), (xC1, yC1, zC1), (xC2, yC2, zC2), (xC3, yC3, zC3)}
Грань D = {(xD0, yD0, zD0), (xD1, yD1, zD1), (xD2, yD2, zD2), (xD3, yD3, zD3)}
Грань Е = {(xЕ0, yЕ0, zЕ0), (xЕ1, yЕ1, zЕ1), (xЕ2, yЕ2, zЕ2), (xЕ3, yЕ3, zЕ3)}
Грань F = {(xF0, yF0, zF0), (xF1, yF1, zF1), (xF2, yF2, zF2), (xF3, yF3, zF3)}
Схематично это изобразим на рисунке 2.
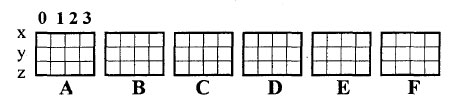
Рис.2. Отдельные грани
В компьютерной программе такой способ описания объекта можно реализовать разнообразно. Например, для каждой грани открыть в памяти отдельный массив. Можно все грани записывать в один массив - вектор.
А можно использовать классы, как для описания отдельных граней, так и объектов в целом. Можно создавать структуры, которые объединяют тройки (x, y, z), или сохранять координаты отдельно. В значительной мере это относится уже к компетенции программиста, зависит от его вкуса. Принципиально это мало что изменяет - так или иначе в памяти необходимо сохранять координаты вершин граней плюс некоторую информацию в качестве накладных затрат.
Рассчитаем объем памяти, необходимый для описания куба следующим образом:
П1 = 6 х 4 х 3 х Рв,
Шесть граней здесь описываются 24 вершинами. Такое представление избыточно - каждая вершина записана трижды. Не учитывается то, что у граней есть общие вершины.
На следующем шаге мы рассмотрим второй способ представления этой модели.
