На этом шаге мы рассмотрим алгоритм выполнения этой операции.
Рассматривая модели отражения света, можно сделать вывод, что нормаль к поверхности является важным элементом. Определение вектора нормали к поверхности в заданной точке может быть выполнено различными способами. В значительной степени это определяется типом модели описания поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных производных функций описания. Например, если поверхность задана параметрическими функциями
x=x(s, t), y=y(s, t), z=z(s, t),
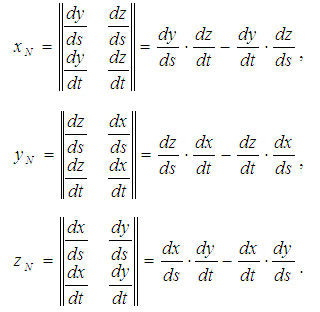
В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.
Пусть в пространстве задана некоторая многогранная поверхность. Рассмотрим одну ее плоскую грань в виде треугольника (рисунок 1).
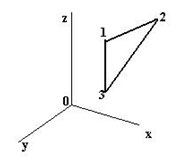
Рис.1. Одна грань поверхности
Для вычисления координат вектора нормали воспользуемся векторным произведением любых двух векторов, лежащих в плоскости грани. В качестве таких векторов могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены только для радиус-векторов.
Чтобы перейти к радиус-векторам, введем новую систему координат, центр которой совпадает с вершиной 1, а оси параллельны осям прежней системы.
Координаты вершин в новой системе:
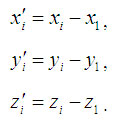
Теперь назовем ребро (1-2) вектором А, а ребро (1-3) - вектором В, как показано на рисунке 2.
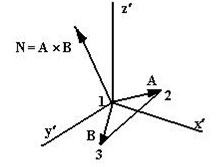
Рис.4. Радиус-векторы
Таким образом, положение нормали к грани в пространстве будет описываться радиус-вектором N. Его координаты в системе (x', y', z') выразим формулами для векторного произведения:
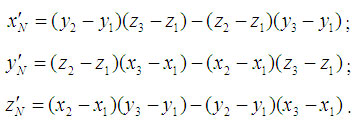
Здесь использованы координаты вершин грани до переноса.
Плоская грань может изображаться в различных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, соответствующее видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать в качестве нормали обратный вектор, то есть (-N).
Если полигональная поверхность имеет не треугольные грани, а, например, плоские четырехугольные, то расчет нормаль можно выполнять по любым трем вершинам грани.
На следующем шаге мы закончим рассматривать диффузное отражение.
