На этом шаге мы зкончим рассматривать эту модель отражения.

    Определим косинус угла между вектором нормали и направлением на источник света.

    Первый пример (возможно, самый простой). Источник света располагается на оси z в бесконечности. Если расчеты производятся для видовой системы координат, то это означает, что источник света располагается на одной оси с камерой.

    Косинус угла нормали к грани с осью z равен отношению координаты z и длины радиус-вектора:

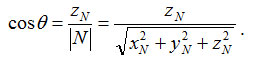
    Второй пример. Источник света располагается в бесконечности и не лежит на оси z. В этом случае существенным является способ задания направления на источник света. Если расположение источника света описывать так же, как и для камеры - двумя углами α_c и β_c, то можно сделать поворот координат так, чтобы ось z была направлена на источник света, и применить формулы для первого примера. Иными словами, необходимо преобразовать координаты вектора нормали. Здесь можно использовать тот факт, что длина вектора при повороте не изменяется, поэтому достаточно вычислить координату в повернутой системе координат.

    Если расположение источника света описывается вектором, направленным на источник света, то косинус угла с вектором нормали можно вычислить следующим образом. Вначале необходимо определить радиус-вектор, направленный на источник света. Обозначим его как S. Затем, для вычисления косинуса угла между радиус-векторами S и N воспользуемся формулами скалярного произведения векторов. Так как:

  S * N = |S| |N| cos θ  ,

  S * N =  xS xN + yS yN + zS zN  ,

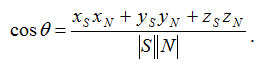
    Третий пример. Источник света располагается в конечной точке пространства с координатами (x_c, y_c, z_c). Для определения косинуса угла с нормалью выполним сдвиг координат источника света так, чтобы вектор нормали в точке поверхности и вектор, направленный на источник света, выходили из общего центра. На предыдущих шагах уже рассматривалось построение радиус-вектора нормали к треугольной грани путем сдвига (параллельного переноса) координат на (-x₁, -y₁, -z₁). Радиус-вектор, который направлен на источник света, и который можно использовать для расчетов, будет иметь координаты (x_c-x₁, y_c-y₁, z_c-z₁). Затем уже можно вычислить искомый косинус угла через скалярное произведение радиус-векторов, как в предыдущем примере.

    На следующем шаге мы рассмотрим зеркальное отражение.

Предыдущий шаг Содержание Следующий шаг