На этом шаге мы рассмотрим особенности реализации этой модели.
Будем считать, что задан радиус-вектор S, направленный на источник света, а также известен радиус-вектор нормали N. Требуется найти косинус угла между отраженным лучом и направлением камеры.
Вначале необходимо вычислить радиус-вектор отраженного луча. Обозначим его как R. Выполним некоторые геометрические построения, как показано на рисунке 1.
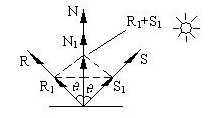
Рис.1. Векторы R1, S1 и N1 - единичной длины
Для решения данной задачи вначале рассмотрим единичные векторы R1, S1 и N1. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно записать R1+ S1 = N', где N'- это вектор, соответствующий диагонали ромба и совпадающий по направлению с нормалью. Длина вектора N' равна 2cosθ. Так как вектор N' по направлению совпадает с N1, то
N' = N12cosθ ,
R1 + S1 = N12cosθ .
Отсюда найдем единичный вектор отраженного луча:
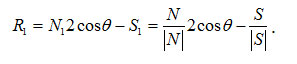
Найдем cosθ. Это можно сделать, используя скалярное произведение векторов N и S:
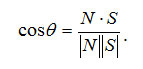
Подставим это значение в выражение для R1:
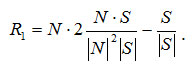
Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, то есть R = |S|R1, получим:
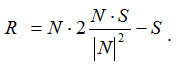
Это решение в векторной форме. Запишем координаты вектора R.
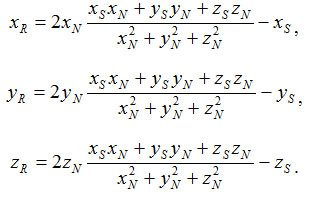
Теперь осталось найти косинус угла между отраженным лучом и направлением камеры. Обозначим радиус-вектор, направленный на камеру, как K. Искомый косинус угла найдем, используя скалярное произведение векторов K и R:
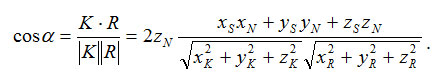
Очевидно, что для упрощения вычислений целесообразно задавать векторы S, N и K единичной длины (тогда и R будет единичным).
На следующем шаге мы рассмотрим метод Гуро.
