На этом шаге мы рассмотрим общий принцип получения изображения методом обратной трассировки.
Рассмотрим, как можно получить растровое изображение некоторой трехмерной сцены методом обратной трассировки. Предположим, что плоскость проецирования разбита на множество квадратиков - пикселей. Выберем центральную проекцию с центром схода на некотором расстоянии от плоскости проецирования. Проведем прямую линию из центра схода через середину квадратика (пикселя) плоскости проецирования (рисунок 1).
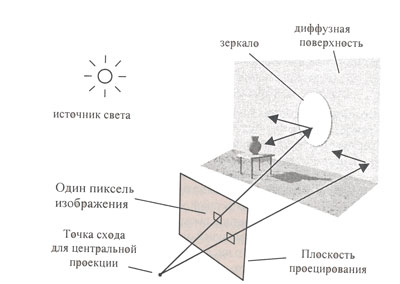
Рис.1. Схема обратной трассировки лучей
Это будет первичный луч обратной трассировки. Если прямая линия этого луча попадает в один или несколько объектов сцены, то выбираем ближайшую точку пересечения. Для определения цвета пикселя изображения нужно учитывать свойства объекта, а также то, какое световое излучение приходится на соответствующую точку объекта.
Если объект зеркальный (хотя бы частично), то строим вторичный луч - луч падения, считая лучом отражения предыдущий, первичный трассируемый луч. На предыдущих шагах мы рассматривали зеркальное отражение (67 шаг) и получили формулы для вектора отраженного луча по заданным векторам нормали и луча падения. Но здесь нам известен вектор отраженного луча, а как найти вектор падающего луча? Для этого можно использовать ту же самую формулу зеркального отражения, но определяя необходимый вектор луча падения как отраженный луч. То есть отражение наоборот.
Для идеального зеркала достаточно затем проследить лишь очередную точку пересечения вторичного луча с некоторым объектом. Что означает термин "идеальное зеркало"? Будем полагать, что у такого зеркала идеально ровная отполированная поверхность, поэтому одному отраженному лучу соответствует только один падающий луч. Зеркало может быть затемненным, то есть поглощать часть световой энергии, но все равно остается правило: один луч падает - один отражается. Можно рассматривать также "неидеальное зеркало". Это будет означать, что поверхность неровная. Направлению отраженного луча будет соответствовать несколько падающих лучей (или наоборот, один падающий луч порождает несколько отраженных лучей), образующих некоторый конус, возможно, несимметричный, с осью вдоль линии падающего луча идеального зеркала. Конус соответствует некоторому закону распределения интенсивностей, простейший из которых описывается моделью Фонга - косинус угла, возведенный в некоторую степень. Неидеальное зеркало резко усложняет трассировку - нужно проследить не один, а множество падающих лучей, учитывать вклад излучения от других видимых из данной точки объектов.
Если объект прозрачный, то необходимо построить новый луч, такой, который при преломлении давал бы предыдущий трассируемый луч. Здесь также можно воспользоваться обратимостью, которая справедлива и для преломления. Для расчета вектора искомого луча можно применить ранее приведенные формулы для вектора луча преломления, считая, что преломление происходит в обратном направлении (рисунок 2).
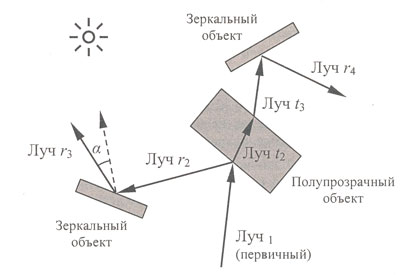
Рис.2. Обратная трассировка для объектов, обладающих свойствами зеркального отражения и преломления
Если объект обладает свойствами диффузного отражения и преломления, то, в общем случае, как и для неидеального зеркала, необходимо трассировать лучи, приходящие от всех имеющихся объектов. Для диффузного отражения интенсивность отраженного света, как известно, пропорциональна косинусу угла между вектором луча от источника света и нормалью. Здесь источником света может выступать любой видимый из данной точки объект, способный передавать световую энергию.
Когда выясняется, что текущий луч обратной трассировки не пересекает какой-либо объект, а уходит в свободное пространство, то на этом трассировка для этого луча заканчивается.
Обратная трассировка лучей в том виде, в каком мы ее здесь рассмотрели, хоть и сокращает перебор, но не позволяет избавиться от бесконечного числа анализируемых лучей. В самом деле, данный метод позволяет сразу получить для каждой точки изображения единственный первичный луч обратной трассировки. Однако вторичных лучей отражения уже может быть бесконечное количество. Так, например, если объект может отражать свет от любого другого объекта, и если эти другие объекты имеют достаточно большие размеры, то какие именно точки излучающих объектов нужно учитывать для построения соответствующих лучей, например, при диффузном отражении? Очевидно, все точки.
На следующем шаге мы рассмотрим продолжим изучение этого вопроса.
