На этом шаге мы рассмотрим алгоритм удаления таких точек.
Для изображения поверхности шара с удалением невидимых точек в аксонометрической проекции можно воспользоваться таким свойством: видимыми являются точки с неотрицательным значением координаты Z в системе видовых координат. При этом центр видовых координат (X, Y, Z) совпадает с центром шара, плоскость X0Y является плоскостью проецирования, а ось Z направлена на камеру (наблюдателя). На рисунке 1 приведен простейший вариант показа поверхности шара с удалением невидимых точек меридианов и параллелей.
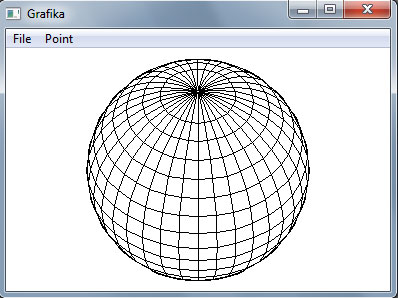
Рис.1. Удалены невидимые точки
Приведенные на этом и предыдущем шагах изображения были построены на основе линий и являются схематичными, весьма далекими от реалистичного изображения поверхности шара. Значительно лучше можно нарисовать шар с помощью фигур с заполнением - закрашиванием поверхности разными цветами.
В заключение этого шага приведем текст программы, которая строит вращающийся шар (рисунок 1).
. . . . void MerOrPar(HDC hdc,int cxw,int cyw,double R, double alf, double bt, BOOL mer); void DrawMyEh(HDC hdc, double alf, double bt, int cxw, int cyw); void RotXYZ(double *X, double *Y, double *Z, double x, double y, double z, double a, double b); void DrawStudyExample(HWND hWnd) { HDC hdc, hdcWin; RECT rc; HBITMAP hBitMap; HCURSOR hCurOld; hCurOld=SetCursor(LoadCursor(NULL,IDC_WAIT)); GetClientRect(hWnd,&rc); hdcWin=GetDC(hWnd); hdc=CreateCompatibleDC(hdcWin); hBitMap=CreateCompatibleBitmap(hdcWin, rc.right, rc. bottom); SelectObject(hdc, hBitMap); PatBlt(hdc, 0,0,rc.right,rc.bottom, WHITENESS); for(int alf=0;alf<=720;alf++) { DrawMyEh(hdc,alf,45,rc.right,rc.bottom); BitBlt(hdcWin,0,0,rc.right,rc.bottom, hdc,0,0,SRCCOPY); } DeleteDC(hdc); DeleteObject(hBitMap); ReleaseDC(hWnd,hdcWin); SetCursor(hCurOld); } void MerOrPar(HDC hdc,int cxw,int cyw,double R, double alf, double bt, BOOL mer) { int i,j, st_i,end_i, st_j,end_j; BOOL st; double x,y,z,X,Y,Z,B,L,rad; double *ai,*aj; rad=M_PI/180.0; alf*=rad; bt*=rad; if(mer) { st_i=0; end_i=360; st_j=-90; end_j=90; ai=&L; aj=&B; } else { st_i=-80; end_i=80; st_j=0; end_j=360; ai=&B; aj=&L; } for (i=st_i;i<end_i;i+=10) { st=FALSE; *ai=(double)i*rad; for(j=st_j;j<=end_j;j+=10) { *aj=(double)j *rad; x=R*cos(B)*sin(L); y=R*cos(B)*cos(L); z=R*sin(B); RotXYZ(&X,&Y,&Z,x,y,z,alf,bt); if(st) { if(Z<0) st=FALSE; else LineTo(hdc,X+cxw/2,Y+cyw/2); } else { if(Z>=0) { st=TRUE; MoveToEx(hdc, X+cxw/2,Y+cyw/2,NULL); } } } } } void DrawMyEh(HDC hdc, double alf, double bt, int cxw, int cyw) { int R; if(cxw<=cyw) R=cxw/2-10; else R=cyw/2-10; Ellipse(hdc, cxw/2-R,cyw/2-R,cxw/2+R,cyw/2+R); MerOrPar(hdc, cxw,cyw,R,alf,bt,TRUE); MerOrPar(hdc, cxw,cyw,R,alf,bt,FALSE); } void RotXYZ(double *X, double *Y, double *Z, double x, double y, double z, double adouble, double b) { *X=x*cos(a)-y*sin(a); *Y=x*sin(a)*cos(b)+y*cos(a)*cos(b)-z*sin(b); *Z=x*sin(a)*sin(b)+y*cos(a)*sin(b)+z*cos(b); }
На следующем шаге мы рассмотрим многогранник с закрашиванием граней.
