На этом шаге мы рассмотрим общие вопросы, связанные с построением многограмнников.
Теперь нарисуем шар в виде многогранника, аппроксимирующего форму поверхности с заданной точностью. Известно большое число типов многогранников. Сведения о них имеются в многочисленных книгах по геометрии.
Мы будем рассматривать достаточно узкий класс многогранников. Отличительным признаком рассматриваемых многогранников является то, что у них ребра ориентированы вдоль меридианов и параллелей. Такие многогранники будем описывать двумя параметрами - шаг по широте (dB) и шаг по долготе (dL) в градусах. Кроме того, будем считать эти многогранники вписанными изнутри в шар, то есть вершины каждой грани лежат на поверхности шара. Очевидно, что с увеличением количества граней такие многогранники все больше приближаются к шару. Иными словами, чем меньше dB и dL, тем лучше поверхность многогранника аппроксимирует форму поверхности шара.
На рисунке 1 приведены примеры таких многогранников.
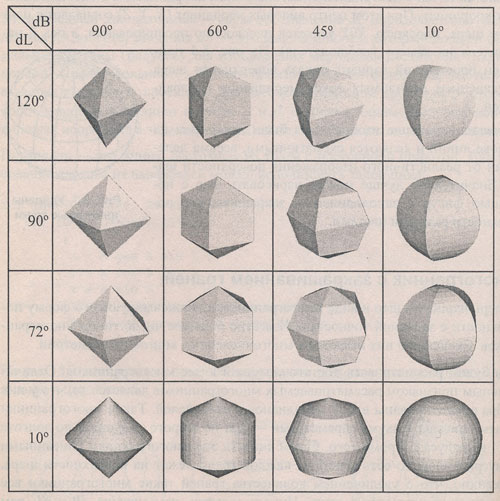
Рис.1. Примеры многогранников
Некоторые из этих многогранников достаточно интересны по форме, а многогранник с параметрами dB = 90°, dL = 90° называется октаэдром.
Все грани, примыкающие к верхнему и нижнему полюсам, являются треугольными, а остальные грани - четырехугольными. С позиций компьютерной графики это выгодно отличает многогранники рассматриваемого типа от других, например, правильных многогранников, у которых грани могут иметь значительно больше ребер, чем четыре.
Для построения изображения многогранников будем рисовать каждую грань как полигон. Для вывода полигона требуется определить координаты всех его вершин и задать цвет заполнения.
Очевидно, что показ граней одним цветом дает неудовлетворительный результат - полностью теряется форма поверхности трехмерного объекта. Показ ребер (контуров полигонов граней) другим цветом немного улучшает восприятие (рисунок 2).
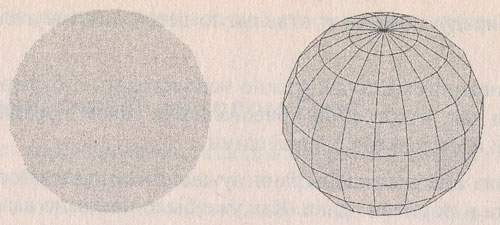
Рис.2. Неудачное изображение - все грани одного цвета
На следующем шаге мы закончим изучение этого вопроса.
