На этом шаге мы рассмотрим расширенную иерарию принятия решений.
Общая структура метода анализа иерархий может включать несколько иерархических уровней со своими критериями.
Предположим в предыдущем примере, что сестра-близнец Мартина Джейн также получила полную стипендию от трех университетов. Однако их родители ставят условие, что дети должны учиться в одном университете, тогда они смогут пользоваться одним автомобилем.
На рис.1 приведена структура задачи выбора решения, которая теперь включает два иерархических уровня со своими критериями.
Величины р и q (предположительно равные) на первом иерархическом уровне представляют собой весовые коэффициенты, которые приписываются точке зрения Мартина и Джейн относительно процесса выбора соответственно.
Второй иерархический уровень использует веса (р1, р2) и (q1, q2) для отображения индивидуальных точек зрения Мартина и Джейн относительно критериев местонахождения и академической репутации каждого университета.
Остальная часть структуры принятия решения может быть интерпретирована аналогично предыдущему примеру. Заметим, что p + q = 1, p1 + p2 = 1, q1 + q2 = 1, p11 + p12 + p13 = 1, p21 + p22 + p23 = 1, q11 + q12 + q13 = 1, q21 + q22 + q23 = 1 комбинированного веса для университета А, представленное на рис. 1, демонстрирует, каким образом вычисляются эти показатели.
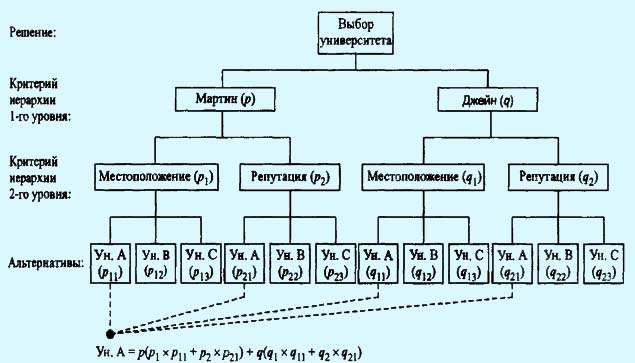
Рис.1. Расширенная иерархияпринятия решений
Задание 1.
Пусть для задачи выбора университета Мартином и Джейн установлены следующие значения весовых коэффициентов.
р=0,5, q=0,5,
p1=0,17, p2=0,83,
p11=0,129, p12=0,277, p13=0,594,
p21=0,545, p22=0,273, p23=0,182,
q1=0,3, q2=0,7,
q11=0,2, q12=0,3, q13=0,5,
q21=0,5, q22=0,2, q23=0,3,
Решение и комментарии вы можете посмотреть здесь.
На следующем шаге мы рассмотрим способы определения весовых коэффициентов.
