На этом шаге мы рассмотрим модель чистой гибели.
В данной модели предполагается, что система начинает функционировать, когда в момент времени t в ней имеется N клиентов и не допускается ни одного нового поступления клиента. Обслуженные клиенты выбывают из системы с интенсивностью μ клиентов в единицу времени. Пусть pn(t) — вероятность того, что после t временных единиц в системе остается n клиентов. Для получения разностно-дифференциальных уравнений относительно pn(t) обычно следуют логике рассуждений, использованных в модели чистого рождения (шаг 80). Поэтому имеем
pN(t + h) = pN(t)(1 - μh),
pn(t + h) = pn(t)(1 - μh) + pn+1(t)μh, 0 < n < N,
p0(t + h) = p0(t) + p1(t)μh.
При h → 0 получим
pN'(t) = - μpN(t),
pn'(t) = - μpn(t) + μpn+1(t), 0 < n < N,
p0'(t) = μp1(t).
Эти уравнения имеют решение
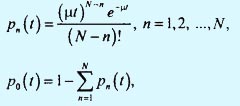
которое называется усеченным распределением Пуассона.
На следующем шаге мы рассмотрим применение и реализацию с помощью TORA модели чистой гибели.
