На этом шаге мы рассмотрим применение и реализацию с помощью TORA модели чистой гибели.
Секция цветов бакалейно-гастрономического магазина складирует 18 дюжин роз в начале каждой недели. В среднем продается 3 дюжины роз в день (за один раз продается дюжина роз), но действительный спрос подчиняется распределению Пуассона. Как только уровень запаса снижается до 5 дюжин, делается новый заказ на поставку 18 дюжин роз в начале следующей недели. Запасы по своей природе таковы, что все неиспользованные до конца недели розы приходят в негодность и ликвидируются. Требуется вычислить следующие параметры системы.
- Вероятность размещения заказа к концу каждого дня недели.
- Среднее количество роз, которые будут ликвидированы к концу недели.
Так как розы покупаются с интенсивностью μ = 3 дюжины в день, то вероятность того, что заказ будет размещен в конце дня t, равна
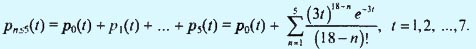
Для расчетов воспользуемся программой TORA. Пункт меню Queuing analysis.
Исходный файл можно взять здесь.
Выбираем из списка Select output option - Scenario1.
В таблице (см. рис. 1) выбираем значение P(n) при n = 5 (т.к новый заказ делается, как только уровень
запаса снижается до 5 дюжин)
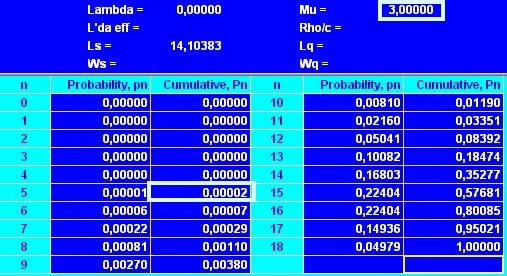
Рис. 1. Вероятность размещения заказа к концу 1 дня
В таблице (см. рис. 2) выбираем значение P(n) при n = 5
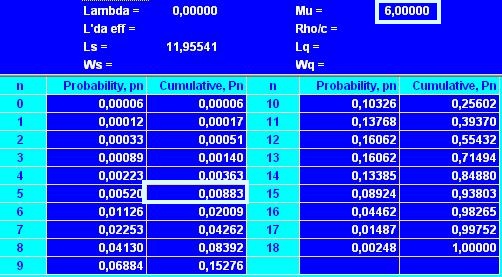
Рис. 2. Вероятность размещения заказа к концу 2 дня
В таблице (см. рис. 3) выбираем значение P(n) при n = 5
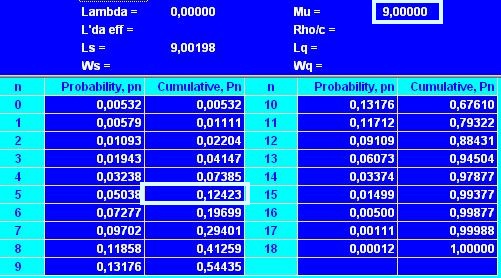
Рис. 3. Вероятность размещения заказа к концу 3 дня
В таблице (см. рис. 4) выбираем значение P(n) при n = 5
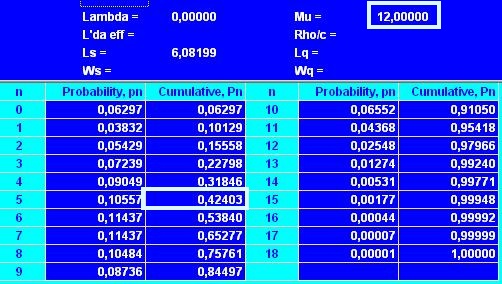
Рис. 4. Вероятность размещения заказа к концу 4 дня
В таблице (см. рис. 5) выбираем значение P(n) при n = 5
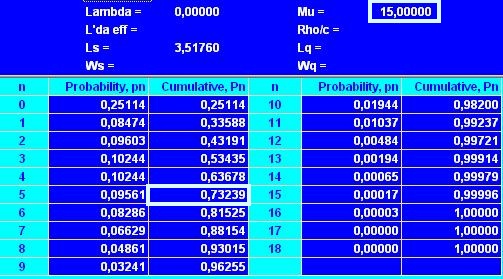
Рис. 5. Вероятность размещения заказа к концу 5 дня
В таблице (см. рис. 6) выбираем значение P(n) при n = 5
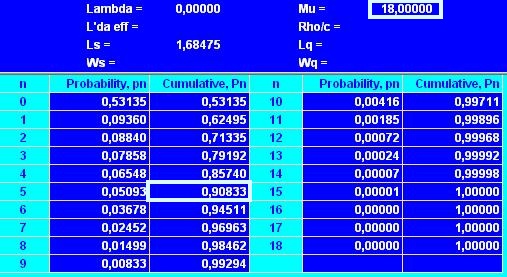
Рис. 6. Вероятность размещения заказа к концу 6 дня
В таблице (см. рис. 7) выбираем значение P(n) при n = 5
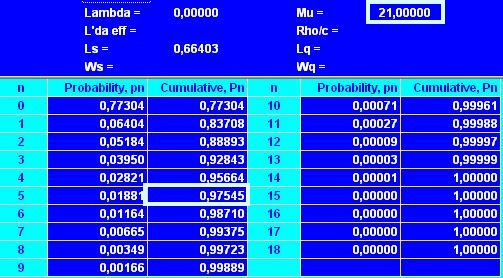
Рис. 7. Вероятность размещения заказа к концу 7 дня
Оформим полученные данные в таблицу:
| t (дни) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| μt | 3 | 6 | 9 | 12 | 15 | 18 | 21 |
| pn ≤ 5(t) | 0,0000 | 0,0088 | 0,1242 | 0,4240 | 0,7324 | 0,9083 | 0,9755 |
Среднее количество роз, которые будут ликвидированы к концу недели (t = 7), вычисляется следующим образом.
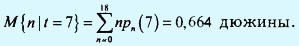
На следующем шаге рассмотрим общую модель системы массового обслуживания.
