На этом шаге мы рассмотрим общую модель системы массового обслуживания.
В общей моделе системы массового обслуживания в существует как входной поток клиентов, так и выходной поток обслуженных клиентов. Время между последовательными поступлениями клиентов и время обслуживания являются экспоненциально распределенными случайными величинами. Эта модель служит основой при рассмотрении специализированных моделей Пуассона, которым посвящен шаг 88.
При рассмотрении общих систем массового обслуживания предполагается, что система функционирует в течение достаточно большого интервала времени, по истечении которого в ее работе наступает стационарный режим. Этот режим функционирования обслуживающей системы противопоставляется переходному (или неустановившемуся) режиму, который превалирует в самый начальный период функционирования системы.
В рассматриваемой общей модели системы массового обслуживания предполагается, что и интенсивность поступления клиентов, и интенсивность выходного потока зависят от состояния системы, что означает их зависимость от числа клиентов в системе обслуживания. Например, сборщик платы за проезд по автомагистрали в часы интенсивного движения стремится ускорить сбор пошлины. Или в мастерской с фиксированным количеством станков интенсивность их поломки убывает по мере возрастания числа аварийных станков, ибо лишь работающие станки могут выходить из строя.
Введем следующие обозначения.
n - число клиентов в системе обслуживания (в очереди и на обслуживании),
λn - интенсивность поступления в систему клиентов при условии, что в системе
уже находится п клиентов,
μn - интенсивность выходного потока обслуженных клиентов при условии,
что в системе находится n клиентов,
pn - вероятность того, что в системе находится n клиентов.
В общей модели системы массового обслуживания устанавливается функциональная зависимость вероятностей pn от λn и μn. Эти вероятности используются затем при определении функциональных характеристик обслуживающей системы, таких как средняя длина очереди, среднее время ожидания и средний коэффициент использования сервисов.
Вероятности pn определяются из диаграммы интенсивностей переходов, представленной на рис. 1. Обслуживающая система находится в состоянии n, если в ней имеется n клиентов. Вероятность появления более одного нового клиента на протяжении малого промежутка времени h стремится к нулю при h → 0. Это означает, что при n > 0 состояние n может быть изменено в двух возможных направлениях: n - 1, когда с интенсивностью μn обслуженный клиент выбывает из системы, и n + 1, когда клиенты поступают с интенсивностью λn. Состояние 0 может измениться лишь к состоянию 1, когда имеет место поступление клиента с интенсивностью λ0. Заметим, что μ0 не определено, так как клиенты не могут выбывать из пустой системы обслуживания.
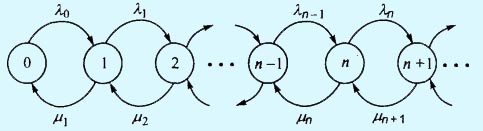
Рис. 1. Диаграмма интенсивностей переходов
При выполнении условий стационарности ожидаемые интенсивности входного и выходного потоков в состоянии n (n > 0) должны быть равны. Так как состояние n может изменяться лишь к состояниям n - 1 и n + 1, отсюда следует
(ожидаемая интенсивность входного потока в состоянии n) = λn-1pn-1 + μn+1pn+1.
Аналогично
(ожидаемая интенсивность выходного потока в состоянии n) = (λn + μn)pn.
Приравнивая эти две интенсивности, получаем следующее уравнение баланса.
λn-1pn-1 + μn+1pn+1 = (λn + μn)pn, n = 1, 2, ...
Как видно из рис. 1, уравнение баланса, соответствующее n = 0, имеет вид λ0p0 = μ1p1
Уравнения баланса решаются рекуррентно, последовательно выражая вероятности р, через р0 следующим образом: для n = 0 имеем p1 = (λ0/μ1)p0
Для n = 1 получаем λ0p0 + μ2p2 = (λ1 + μ1)p1
Подставляя сюда p1 = (λ0/μ1)p0 и упрощая полученное выражение, имеем p2 = (λ0λ1/μ1μ2)p0
Методом индукции можно показать, что pn = (λ0λ1...λn-1/μ1μ2...μn)p0, n = 1, 2, ...
Значение p0 определяется из уравнения ∑pn = 1, n = 0, 1, 2, ...
На следующем шаге рассмотрим применение общей модели массового обслуживания.
