На этом шаге мы рассмотрим применение общей модели массового обслуживания.
Бакалейный магазин работает с тремя кассами. Вывеска возле касс извещает покупателей, что в любой момент будет открыта дополнительная касса, как только число покупателей в любой очереди превысит 3. Это означает, что если число покупателей меньше четырех, то работать будет лишь одна касса. Если число покупателей от четырех до шести, то будет работать две кассы. Если имеется больше шести покупателей, будут открыты все три кассы. Покупатели подходят к кассам в соответствии с распределением Пуассона с математическим ожиданием 10 человек в час. Время обслуживания одного покупателя в кассе распределено по экспоненциальному закону со средним 12 минут. Определим в установившемся режиме вероятность рn, что n покупателей стоят в очереди в кассу.
Из формулировки задачи имеем следующее.

Следовательно,
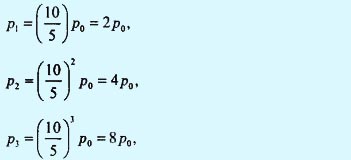
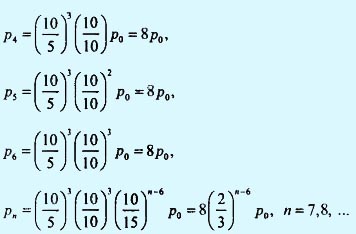
Значение р0 определяется из уравнения
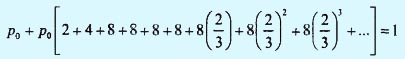
или, что равносильно,
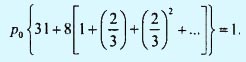
Используя формулу суммы бесконечной геометрической прогрессии
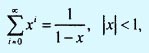
получаем следующее.
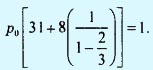
Следовательно, р0 = 1/35.
Зная р0, можно определить любую вероятность, имеющую отношение к задаче. Например, вероятность того, что будет работать лишь одна касса, вычисляется как вероятность нахождения в системе не больше трех клиентов, т.е.
р0 + р1 + р2 + р3 = (1 + 2 + 4 + 8)(1/35) = 0,273.
Здесь предполагается, что в бакалейном магазине будет открыта как минимум одна касса, даже в том случае, когда вовсе нет покупателей.
Вероятности рn можно использовать для определения численных значений функциональных характеристик рассматриваемой системы. Например, среднее количество неработающих касс равно
3р0 + 2(р1 + р2 + р3) + 1(р4 + р5 + р6) + 0(р7 + р8 + ...) = 1 касса
На следующем шаге рассмотрим специализированные системы обслуживания с пуассоновским распределением.
