На этом шаге мы рассмотрим применение одноканальной модели с пуассоновским входным потоком.
Автоматическая мойка для автомобилей имеет только один моечный бокс. Автомобили прибывают в соответствии с распределением Пуассона со средним 4 машины в час и могут ожидать обслуживания на стоянке рядом с автомойкой. Время мойки автомобиля является экспоненциально распределенной случайной величиной с математическим ожиданием 10 мин. Автомобили, которые не помещаются на стоянке, могут ожидать на прилегающей к автомойке улице. Это значит, что практически нет ограничений на емкость системы обслуживания. Хозяин автомойки хочет определить количество мест на стоянке для автомобилей.
Для рассматриваемой задачи имеем λ = 4 автомобиля в час и μ = 60/10 = 6 автомобилей в час. Так как ρ = λ/μ < 1, то система может функционировать в стационарном режиме.
Результаты использования программы TORA для решения рассматриваемой задачи, представленные на рис. 1, получены путем введения данных в следующем порядке: λ = 4, μ = 6, с = 1, емкость системы равна ∞ и емкость источника также равна ∞.
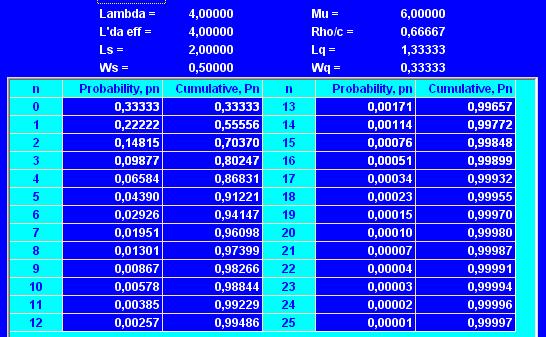
Рис. 1. Результаты решения
Исходный файл можно взять здесь.
Результаты решения показывают, что среднее количество автомашин, ожидающих в очереди, равно Lq = 1,33 автомашины. Мы не можем рассматривать Lq в качестве единственного аргумента при определении искомого количества мест на стоянке, ибо при расчете должна учитываться максимально возможная длина очереди. Например, можно рассчитать количество мест на стоянке, при котором по меньшей мере 90 % прибывших автомобилей найдет место на стоянке.
Пусть неизвестная переменная s представляет искомое количество мест на стоянке. Тогда система имеет емкость s + 1 (очередь плюс место на мойке). Прибывающий автомобиль в 90 % случаев получит место на стоянке, если в системе находится максимум s автомобилей. Это условие эквивалентно следующему вероятностному утверждению:
p0 + p1 + ... + ps ≥ 0,9
Из таблицы, показанной на рис. 1, следует, что суммы вероятностей рn равны 0,86831 и 0,91221 при n = 4 и n = 5 соответственно. Это значит, что условие выполняется при s > 5 мест на стоянке. Количество мест на стоянке s может быть также определено с использованием формулы, определяющей рn. Получаем
(1 - ρ)(1 + ρ + ρ2 + ... + ρs) ≥ 0,9
Сумма усеченного геометрического ряда равна (1 - ρs+1)/(1 - ρ). Следовательно, последнее выражение приводится к виду (1 - ρs+1) > 0,9. Упрощая это неравенство, получаем ρs+1 < 0,1.
Логарифмируя обе части последнего неравенства, получаем следующее s ≥ ln(0,1)/ln(4/6) - 1 = 4,679 ≈ 5. Таким образом, необходимо s ≥ 5 мест на стоянке.
На следующем шаге мы приведем несколько задач.
