На этом шаге представлены две модели обслуживающей системы с одним средством обслуживания (т.е. с = 1).

Предполагается, что клиенты поступают с постоянной интенсивностью λ. Интенсивность обслуживания также постоянна и равна μ клиентов в единицу времени. Первая модель не устанавливает ограничений на вместимость системы, во второй модели предполагается, что вместимость системы является ограниченной. В этих двух моделях источник, "порождающий" клиентов, имеет неограниченную емкость.

Используем обозначения Кендалла, чтобы описать характеристики системы обслуживания в каждом случае. Так как вывод выражения для р_n на шаге 86 и всех функциональных характеристик обслуживающей системы выполнен независимо от конкретной дисциплины очереди, в обозначениях будем использовать символ GD (дисциплина очереди не регламентирована).

Модель (М / М / 1) : (GD / ∞ / ∞).

Используя обозначения общей модели, имеем λ_n = λ и μ_n = μ для всех n = 0, 1, 2, ...

Поскольку отсутствуют ограничения на емкость очереди, и, следовательно, все прибывающие клиенты могут попасть в систему обслуживания, то λ_эфф = λ и λ_потери = 0. Обозначим ρ = λ / μ. Тогда выражение для вероятности р_n в общей модели принимает следующий вид: p_n = ρⁿp₀, n = 0, 1, 2, ...

Для определения величины р₀ используется тождество p₀(1 + ρ + ρ² + ...) = 1.

Предполагаем, что ρ < 1, тогда геометрический ряд имеет конечную сумму 1/(1 - ρ), поэтому р₀ = 1 - ρ. Следовательно, общая формула для р_n имеет вид р_n = (1 - ρ)ρⁿ, n = 1, 2, ..., ρ < 1.

Эти значения вероятностей р_n (включая вероятность р₀) соответствуют геометрическому распределению.

При выводе формулы для р_n предполагалось, что ρ < 1. Это означает, что для достижения системой стационарного режима функционирования необходимо, чтобы интенсивность поступления клиентов λ была строго меньше интенсивности обслуживания μ. Если λ ≥ μ, геометрический ряд является расходящимся, и, следовательно, вероятности р_n стационарного состояния не существуют. В этом случае система обслуживания будет функционировать в нестационарном режиме, когда длина очереди со временем неограниченно возрастает.

Среднее число находящихся в системе клиентов L как функциональная характеристика обслуживающей системы вычисляется по следующей формуле:

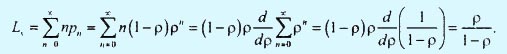
Так как в рассматриваемой модели λ_эфф = λ, то остальные функциональные характеристики обслуживающей системы вычисляются с использованием соотношений из шага 89, что приводит к следующим результатам:

   W_s = L_s/λ = 1/[μ(1 - ρ)] = 1/(μ - λ),
   W_q = W_s - 1/μ = ρ/[μ(1 - ρ)],
   L_q = λW_q = ρ²/(1 - ρ),
    = L_s - L_q = ρ.

На следующем шаге мы рассмотрим применение одноканальной модели с пуассоновским входным потоком.

Предыдущий шаг Содержание Следующий шаг