На этом шаге мы рассмотрим одноканальную модель системы массового обслуживания с ожиданием и не более, чем c N клиентами.
Модель (М / М / 1) : (GD / N/ ∞)
Эта модель отличается от рассмотренной выше только тем, что система вмещает не более N клиентов (максимальная длина очереди равняется N - 1). Примерами обслуживающей системы такого типа служат производственные ситуации, когда станок может иметь ограниченную зону складирования заготовок, а также рестораны быстрого питания с одним пунктом обслуживания клиентов на автомобилях и т.д.
Ситуация в рассматриваемой модели такова, что, как только число клиентов в системе достигает N, ни один из дополнительных клиентов на обслуживание не принимается. Из этого условия следует, что при n = 0, 1, ..., N - 1 λn = λ, а при n = N, N + 1, ... λn = 0, при любом n μn = μ.
Используя обозначение ρ = λ/μ имеем при n ≤ N, pn = ρnp0, иначе pn = 0.
Значение вероятности р0 определяется из уравнения ∑pn = 1 при n = 0, 1, ..., ∞, которое принимает следующий вид: p0(1 + ρ + ρ2 + ... + ρN) = 1.
Отсюда получаем, что при ρ ≠ 1, p0 = (1 - ρ)/(1 - ρN + 1), иначе p0 = 1/(N + 1).
Следовательно, при ρ ≠ 1, pn = [(1 - ρ)ρn]/(1 - ρN + 1), иначе pn = 1/(N + 1), где n = 0, 1, ..., N.
Заметим, что в этой модели значение параметра ρ = λ/μ не обязательно должно быть меньше единицы, так как поступления клиентов в систему контролируются максимальной емкостью системы N. Это значит, что в данном случае в качестве интенсивности поступления клиентов скорее выступает λэфф, нежели λ. Так как клиенты будут потеряны в том случае, если в системе находится N клиентов: λпотери = λpN, λэфф = λ - λпотери = λ(1 - pN).
Следует ожидать, что λэфф будет меньше μ. Среднее число клиентов в системе вычисляется по формуле
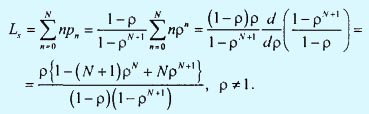
При ρ = 1 Ln = N/2. Используя значения Ls и λэфф, можно также получить выражения для Ws, Wq и Lq, как это сделано на шаге 89.
На следующем шаге мы рассмотрим применение одноканальной модели СМО с ожиданием и не более, чем c N клиентами.
