На этом шаге мы рассмотрим многоканальную модель системы массового обслуживания с ожиданием.
Модель (М / М / с) : (GD / N / ∞), c < N.
Эта модель обслуживающей системы отличается от модели (М / М / с) : (GD / ∞ / ∞) тем, что емкость системы ограничена сверху значением N (тогда максимальная длина очереди равна N - c). Интенсивности поступления и обслуживания клиентов равны λ и μ соответственно. Эффективная интенсивность поступления заявок в систему обслуживания λэфф меньше λ в силу ограниченности емкости системы значением N.
Параметры λn и μn общей модели обслуживающей системы в данной модели определяются следующим образом:
λn = λ, 0 ≤ n < N,
λn = 0, n ≥ N
μn = nμ, 0 ≤ n < c,
μn = cμ, c ≤ n ≤ N.
Подставляя λn и μn в общее выражение для рn из шагa 86 и используя обозначение ρ = λ/μ, получаем
pn = (ρn/n!)p0, 0 ≤ n < c,
pn = (ρn/[c!cn-c])p0, c ≤ n ≤ N.
где
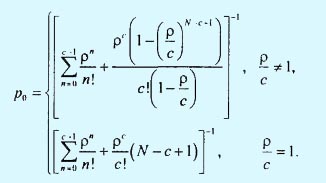
Далее мы вычисляем Lq для ситуации, когда ρ/с ≠ 1:
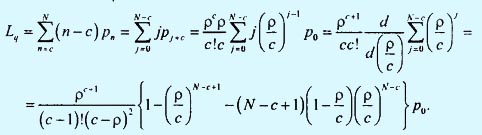
Можно также показать, что для ситуации, когда ρ/с = 1, выражение для Lq имеет следующий вид:
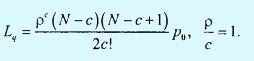
Для определения Wq и, следовательно, Ws и Ls, необходимо получить выражение для λэфф. Поскольку ни один клиент не может попасть в систему после того, как достигнут лимит N по ее вместимости, то λпотери = λpN, λэфф = λ - λпотери = λ(1 - pN).
На следующем шаге рассмотрим применение многоканальной модели системы массового обслуживания с ожиданием.
