На этом шаге мы рассмотрим применение многоканальной модели системы массового обслуживания с ожиданием.
Пусть в задаче, связанной с объединением служб такси, которая рассматривалась в примере шага 98, известно, что объединенная служба такси не имеет финансовых возможностей для покупки новых автомашин. Друг нового хозяина советует информировать пассажиров о возможных задержках с прибытием заказанной автомашины, как только список ожидающих клиентов достигает шести. Эта мера, несомненно, заставит новых клиентов искать обслуживания в другом месте, что уменьшит время ожидания тех клиентов, которые уже ожидают в очереди. Необходимо узнать, насколько полезным является совет друга.
Ограничение списка ожидающих в очереди до 6 клиентов равносильно тому, что емкость системы становится равной N = 6 + 4= 10 клиентов. Следовательно, мы имеем дело с системой обслуживания модели (М / М / 4) : (GD / 10 / ∞) с λ = 16 клиентов в час и μ = 5 поездок в час.
На рис. 1 представлены выходные данные, полученные с помощью программы TORA для этой модели.
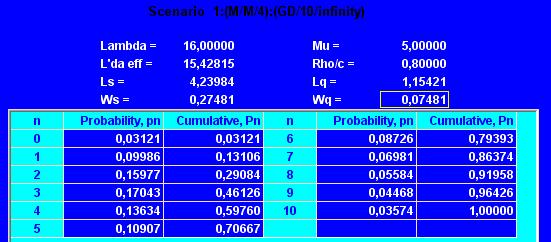
Рис. 1. Выходные данные
Исходный файл можно взять здесь.
Среднее время ожидания Wq при отсутствии ограничения на емкость системы равняется 0,149 ч (≈ 9 мин.) (см. рис. 1 шага 98), что почти в два раза больше значения 0,075 ч (≈ 4,5 мин.) аналогичного показателя при наличии ограничения на емкость системы. Это существенное уменьшение функциональной характеристики системы достигнуто за счет потери примерно 3,6% потенциальных клиентов. Этот результат, однако, не отражает возможной потери расположения клиентов к деятельности службы такси.
На следующем шаге мы приведем решение задачи.
