На этом шаге мы рассмотрим реккурентный алгоритм обратной прогонки.
В примере шага 106 вычисления проводились последовательно: от первого этапа до третьего. Такая последовательность вычислений известна как алгоритм прямой прогонки. Этот же пример может быть решен с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от третьего этапа до первого.
Алгоритмы прямой и обратной прогонки приводят к одному и тому же решению. Несмотря на то что алгоритм прямой прогонки представляется более логичным, в специальной литературе, посвященной динамическому программированию, неизменно используется алгоритм обратной прогонки. Причина этого в том, что в общем случае алгоритм обратной прогонки может быть более эффективным с вычислительной точки зрения. Продемонстрируем использование алгоритма обратной прогонки на примере шага 106. Мы также представим вычисления динамического программирования в компактной табличной форме.
Пример.
Рекуррентное уравнение для алгоритма обратной прогонки в примере шага 106 имеет вид
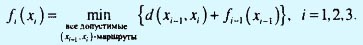
где f4(x4) ≡ 0 для (x4) = 7 Соответствующей последовательностью вычислений будет f3 → f2 → f1.
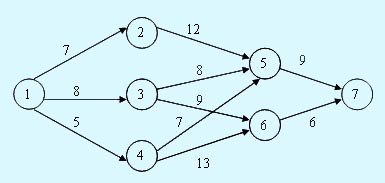
Этап 3.
Поскольку узел 7 (x4 = 7) связан с узлами 5 и 6 (x3 = 5 и 6) только одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.
| x3 | x4 = 7 | f3(x3) | x4 |
|---|---|---|---|
| 5 | 9 | 9 | 7 |
| 6 | 6 | 6 | 7 |
Этап 2.
Так как маршрута (2, 6) не существует, соответствующая альтернатива не рассматривается. Используя значения
f3(x3), полученные на третьем этапе, мы можем сравнить допустимые
альтернативные решения, как показано в следующей таблице.
| x2 | x3 = 5 | x3 = 6 | f2(x2) | x3 |
|---|---|---|---|---|
| 2 | 12 + 9 = 21 | - | 21 | 5 |
| 3 | 8 + 9 = 17 | 9 + 6 = 15 | 15 | 6 |
| 4 | 7 + 9 = 16 | 13 + 6 = 19 | 16 | 5 |
Оптимальное решение второго этапа означает следующее. Если вы находитесь в узле (городе) 2 или 4, кратчайший путь к узлу 7 проходит через узел 5, а если в узле 3 — через узел 6.
Этап 1.
Из узла 1 начинаются три альтернативных маршрута: (1, 2), (1, 3) и (1, 4). Используя значения f2(x2) , полученные на втором этапе, вычисляем данные следующей таблицы. Оптимальное решение на первом этапе показывает, что кратчайший путь проходит через город 4. Далее из оптимального решения на втором этапе следует, что из города 4 необходимо двигаться в город 5. Наконец, из оптимального решения на третьем этапе следует, что город 5 связан с городом 7.
Следовательно, полным маршрутом, имеющим кратчайшую длину, является 1 → 4 → 5 → 7, и его длина равна 21 миле.
| x1 | x2 = 2 | x2 = 3 | x2 = 4 | f1(x1) | x2 |
|---|---|---|---|---|---|
| 1 | 7 + 21 = 28 | 8 + 15 = 23 | 5 + 16 = 21 | 21 | 4 |
На следующем шаге мы рассмотрим задачу о загрузке.
