На этом шаге мы рассмотрим решение задачи линейного программирования в Microsoft Excel.
1. Осуществляем ввод данных в таблицу Excel (рис. 1).
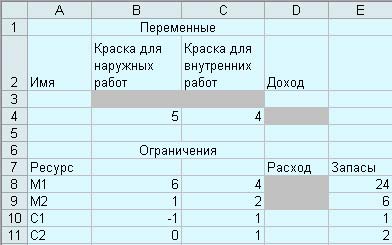
Рис. 1. Заполнение листа для решения задачи
Для переменных задачи x1 и x2 отведены ячейки B3 (имя ячейки - int) и C3 (имя ячейки - ext). Эти ячейки называются рабочими или изменяемыми ячейками. В изменяемые ячейки значения не заносятся и в результате решения задачи в этих ячейках будет отражено оптимальное значение переменной.
В ячейку D4 (имя ячейки - sum) вводится формула для вычисления целевой функции задачи (дохода) z = 5x1 + 4x2. Чтобы сделать это надо выполнить следующие действия:
- поместить курсор в D4;
- вызвать Мастер функций;
- в появившемся окне выбрать "Математические" и "СУММПРОИЗВ" (рис. 2).
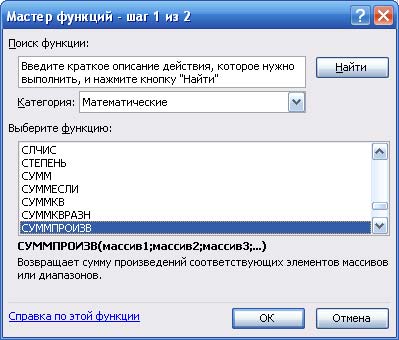
Рис. 2. Мастер функций, Шаг 1 - В окне мастера функций нажать OK, в появившемся окне (рис. 3) в поле "массив 1" ввести (протаскивая курсор мыши по ячейкам) адреса изменяемых ячеек B3:C3. В поле "массив 2" вводятся адреса ячеек содержащих цены на краски B4:C4, после нажать OK.
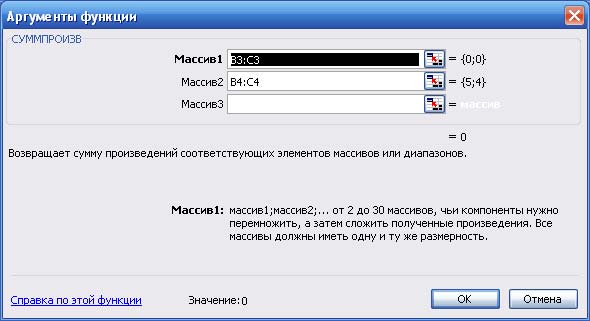
Рис. 3. Мастер функций, Шаг 2 - В ячейку D8 вводится формула для вычисления израсходованного количества сырья M1: 6x1 + 4x2, а в ячейку D9 вводится формула для израсходованного количества сырья M2: x1 + 2x2. В ячейку D10 вводится формула для вычисления спроса на краску: -1x1 + 4x2, а в ячейку D11 вводится формула ограничения на краску для внутренних работ: x2. Эти формулы вводятся аналогично целевой функции.
В результате страница примет вид:
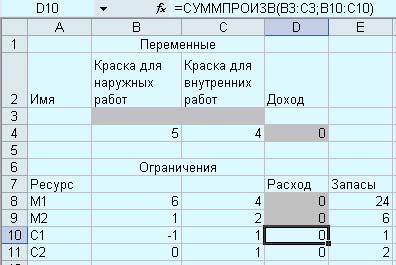
Рис. 4. Вид страницы после добавления формул
2. В меню "Сервис" выбираем процедуру "Поиск решения". В появившемся окне (рис. 5) нужно установить адрес целевой ячейки D4, значение целевой ячейки: максимальное, адреса изменяемых ячеек B3:C3.
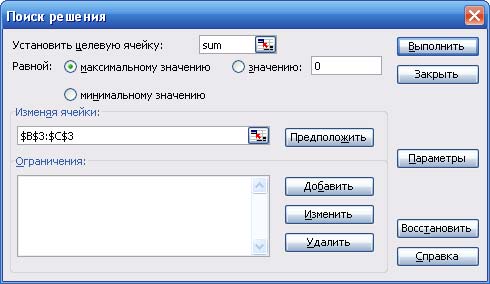
Рис. 5. Поиск решения
3. Чтобы ввести ограничения задачи, нажать кнопку "Добавить". В появившемся диалоговом окне слева ввести адрес D8 (израсходованное количество сырья M1), затем выбрать знак ≤ и в правой части количество сырья M2, равное 24 (или адрес ячейки E8). После ввода нажать кнопку "Добавить" и аналогично ввести второе ограничение.
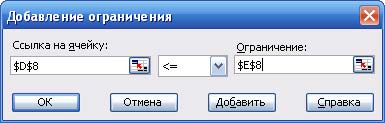
Рис. 6. Добавление ограничения
4. После ввода ограничений получим следующий вид окна поиска решения:
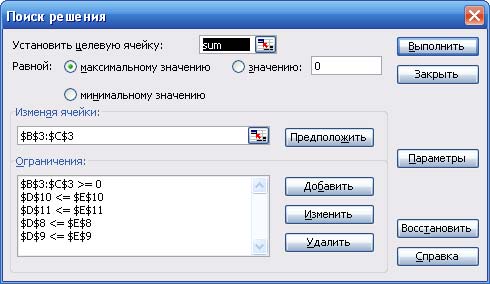
Рис. 7. Результат добавления ограничений
5. В окне "Поиск решения" нажать "Параметры" в появившемся окне (рис. 8) установить флажок в пункте "Линейная модель". В этом случае при решении задачи будет использоваться симплекс - метод. Остальные значения можно оставить без изменения. После нажать кнопку ОК.
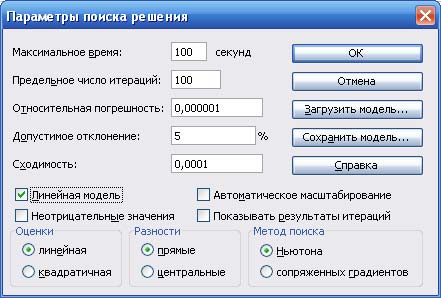
Рис. 8. Окно Параметры
6. Для решения задачи в окне "Поиск решения" нажать кнопку "Выполнить". Если решение найдено появляется окно (рис. 9).
Рис. 9. Результаты поиска решения
7. Для просмотра результатов выбираем тип отчета: "Результаты" и нажимаем кнопку ОК. "Отчет по результатам" состоит из трех таблиц (рис. 10):
- в таблице 1 приводятся сведения о целевой функции;
- в таблице 2 приводятся значения переменных задачи;
- в таблице 3 показаны результаты поиска для ограничений задачи.
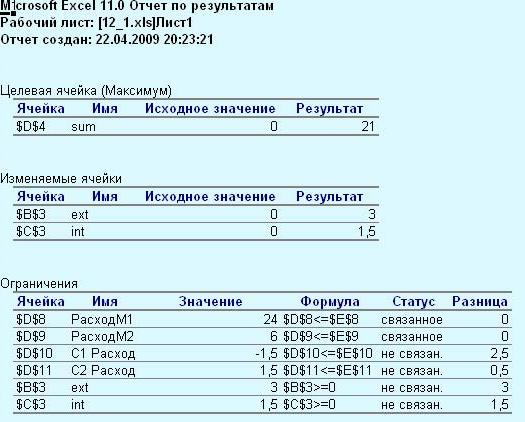
Рис. 10. Отчет Результаты
Из этих таблиц видно, что в оптимальном решении:
производство краски для наружных работ B3 = 3 ;
производство краски для внутренних работ С3 = 1.5 ;
при этом доход D4 = 21 ;
расход сырья М1 D8 = 24 ;
расход сырья М2 D9 = 6 ;
таким образом, оба ресурса дефицитные (соответствующие ограничения называются связанными).
Первоначальная таблица EXCEL заполняется результатами, полученными при решении (рис. 11).
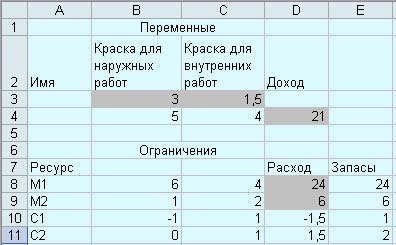
Рис. 11. Результат поиска решения
Файл с решением этой задачи можно взять здесь.
На следующем шаге рассмотрим решение нескольких задач линейного программирования.
