На этом шаге мы проведем анализ KNeighborsClassifier.
Кроме того, для двумерных массивов данных мы можем показать прогнозы для всех возможных точек тестового набора, разместив в плоскости ху. Мы зададим цвет плоскости в соответствии с тем классом, который будет присвоен точке в этой области. Это позволит нам сформировать границу принятия решений (decision boundary), которая разбивает плоскость на две области: область, где алгоритм присваивает класс 0, и область, где алгоритм присваивает класс 1.
Программный код, приведенный ниже, визуализирует границы принятия решений для одного, трех и девяти соседей (показаны на рисунке 1):
[In 14]: import matplotlib.pyplot as plt fig, axes = plt.subplots(1, 3, figsize=(10, 3)) for n_neighbors, ax in zip([1, 3, 9], axes): # создаем объект-классификатор и подгоняем в одной строке clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y) mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4) mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax) ax.set_title("количество соседей:{}".format(n_neighbors)) ax.set_xlabel("признак 0") ax.set_ylabel("признак 1") axes[0].legend(loc=3)

Рис.1. Границы принятия решений, созданные моделью ближайших соседей для различных значений n_neighbors
На рисунке слева можно увидеть, что использование модели одного ближайшего соседа дает границу принятия решений, которая очень хорошо согласуется с обучающими данными. Увеличение числа соседей приводит к сглаживанию границы принятия решений. Более гладкая граница соответствует более простой модели. Другими словами, использование нескольких соседей соответствует высокой сложности модели (как показано в правой части рисунка 2), а использование большого количества соседей соответствует низкой сложности модели (как показано в левой части рисунка 2).
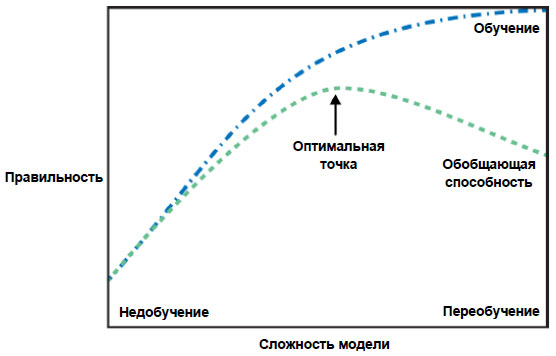
Рис.2. Компромисс между сложностью модели и правильностью на обучающей и тестовой выборках
Если взять крайний случай, когда количество соседей будет равно количеству точек данных обучающего набора, каждая точка тестового набора будет иметь одних и тех же соседей (соседями будет все точки обучающего набора) и все прогнозы будут одинаковыми: будет выбран класс, который является наиболее часто встречающимся в обучающем наборе.
Давайте выясним, существует ли взаимосвязь между сложностью модели и обобщающей способностью, о которой мы говорили ранее. Мы сделаем это с помощью реального набора данных Breast Cancer. Начнем с того, что разобьем данные на обучающий и тестовый наборы. Затем мы оценим качество работы модели на обучающем и тестовом наборах с использованием разного количества соседей. Результаты показаны на рисунках 3 и 4:
from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=66) training_accuracy = [] test_accuracy = [] # пробуем n_neighbors от 1 до 10 neighbors_settings = range(1, 11) for n_neighbors in neighbors_settings: # строим модель clf = KNeighborsClassifier(n_neighbors=n_neighbors) clf.fit(X_train, y_train) # записываем точность на обучающем наборе training_accuracy.append(clf.score(X_train, y_train)) # записываем точность на тестовом наборе test_accuracy.append(clf.score(X_test, y_test)) plt.plot(neighbors_settings, training_accuracy, label="Точность на обучающем наборе") plt.plot(neighbors_settings, test_accuracy, label="Точность на тестовом наборе") plt.ylabel("Точность") plt.xlabel("Количество соседей") plt.legend()
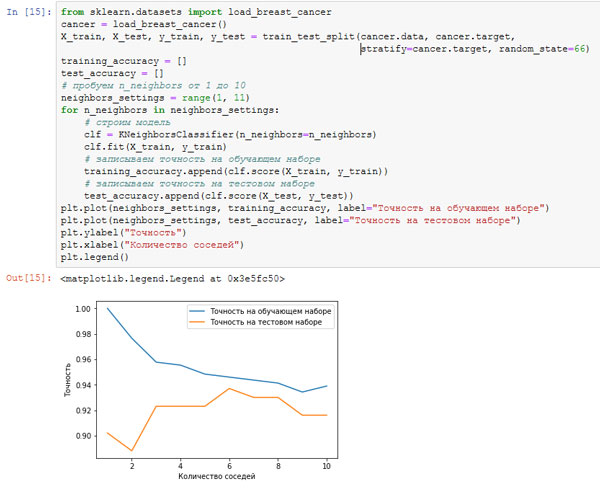
Рис.3. Сравнение правильности на обучающем и тестовом наборах как функции от количества соседей
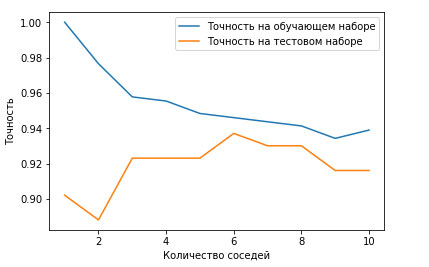
Рис.4. Отдельно график сравнения
На этом графике по оси у отложена правильность на обучающем наборе и правильность на тестовом наборе, а по оси x - количество соседей. В реальности подобные графики редко бывают гладкими, мы по-прежнему можем увидеть некоторые признаки переобучения и недообучения (обратите внимание, что поскольку использование небольшого количества соседей соответствует более сложной модели, график представляет собой изображение рисунке 2, зеркально отраженное по горизонтали). При использовании модели одного ближайшего соседа правильность на обучающем наборе идеальна. Однако при использовании большего количества соседей модель становится все проще и правильность на обучающем наборе падает. Правильность на тестовом наборе в случае использования одного соседа ниже, чем при использовании нескольких соседей. Это указывает на то, что использование одного ближайшего соседа приводит к построению слишком сложной модели. С другой стороны, когда используются 10 соседей, модель становится слишком простой и она работает еще хуже. Оптимальное качество работы модели наблюдается где-то посередине, когда используются шесть соседей. Однако посмотрим на шкалу у. Худшая по качеству модель дает правильность на тестовом наборе около 88%, что по-прежнему может быть приемлемым результатом.
На следующем шаге мы рассмотрим регрессию k ближайших соседей.
