На этом шаге мы рассмотрим особенности реализации этого алгоритма.
Кластеризация k-средних - один из самых простых и наиболее часто используемых алгоритмов кластеризации. Сначала выбирается число кластеров k. После выбора значения k алгоритм k-средних отбирает точки, которые будут представлять центры кластеров (cluster centers). Затем для каждой точки данных вычисляется его евклидово расстояние до каждого центра кластера. Каждая точка назначается ближайшему центру кластера. Алгоритм вычисляет центроиды (centroids) - центры тяжести кластеров. Каждый центроид - это вектор, элементы которого представляют собой средние значения характеристик, вычисленные по всем точкам кластера. Центр кластера смещается в его центроид. Точки заново назначаются ближайшему центру кластера. Этапы изменения центров кластеров и переназначения точек итеративно повторяются до тех пор, пока границы кластеров и расположение центроидов не перестанут изменяться, т.е. на каждой итерации в каждый кластер будут попадать одни и те же точки данных. Следующий пример (рисунок 1) иллюстрирует работу алгоритма на синтетическом наборе данных.
[In 46]:
mglearn.plots.plot_kmeans_algorithm()
Рис.1. Исходные данные и этапы алгоритма k-средних
Центры кластеров представлены в виде треугольников, в то время как точки данных отображаются в виде окружностей. Цвета указывают принадлежность к кластеру. Мы указали, что ищем три кластера, поэтому алгоритм был инициализирован с помощью случайного выбора трех точек данных в качестве центров кластеров (см. "Инициализация"). Затем запускается итерационный алгоритм. Во-первых, каждая точка данных назначается ближайшему центру кластера (см. "Назначение точек (1)"). Затем центры кластеров переносятся в центры тяжести кластеров (см. "Пересчет центров (1)"). Затем процесс повторяется еще два раза. После третьей итерации принадлежность точек кластерным центрам не изменилась, поэтому алгоритм останавливается.
Получив новые точки данных, алгоритм k-средних будет присваивать каждую точку данных ближайшему центру кластера. Следующий пример (рисунок 2) показывает границы центров кластеров, процесс вычисления которых был приведен на рисунке 1:
[In 47]:
glearn.plots.plot_kmeans_boundaries()
Рис.2. Центры кластеров и границы кластеров, найденные с помощью алгоритма k-средних
Применить алгоритм k-средних, воспользовавшись библиотекой scikit-learn, довольно просто. Здесь мы применяем его к синтетическим данным, которые использовали для построения предыдущих графиков. Мы создаем экземпляр класса KMeans и задаем количество выделяемых кластеров.
Если вы не зададите количество выделяемых кластеров, то значение n_clusters по умолчанию будет равно 8. При этом нет никаких конкретных причин, в
силу которых вы должны использовать именно это значение.
Затем мы вызываем метод fit() и передаем ему в качестве аргумента данные:
[In 48]: from sklearn.datasets import make_blobs from sklearn.cluster import KMeans # генерируем синтетические двумерные данные X, y = make_blobs(random_state=1) # строим модель кластеризации kmeans = KMeans(n_clusters=3) kmeans.fit(X)
Во время работы алгоритма каждой точке обучающих данных X присваивается метка кластера. Вы можете найти эти метки в атрибуте kmeans.labels_ :
[In 49]: print("Принадлежность к кластерам:\n{}".format(kmeans.labels_)) Принадлежность к кластерам: [0 1 1 1 2 2 2 1 0 0 1 1 2 0 2 2 2 0 1 1 2 1 2 0 1 2 2 0 0 2 0 0 2 0 1 2 1 1 1 2 2 1 0 1 1 2 0 0 0 0 1 2 2 2 0 2 1 1 0 0 1 2 2 1 1 2 0 2 0 1 1 1 2 0 0 1 2 2 0 1 0 1 1 2 0 0 0 0 1 0 2 0 0 1 1 2 2 0 2 0]
Поскольку мы задали три кластера, кластеры пронумерованы от 0 до 2.
Кроме того, вы можете присвоить метки кластеров новым точкам с помощью метода predict(). В ходе прогнозирования каждая новая точка назначается ближайшему центру кластера, но существующая модель не меняется. Запуск метода predict() на обучающем наборе возвращает тот же самый результат, что содержится в атрибуте labels_:
[In 50]: print(kmeans.predict(X)) [0 1 1 1 2 2 2 1 0 0 1 1 2 0 2 2 2 0 1 1 2 1 2 0 1 2 2 0 0 2 0 0 2 0 1 2 1 1 1 2 2 1 0 1 1 2 0 0 0 0 1 2 2 2 0 2 1 1 0 0 1 2 2 1 1 2 0 2 0 1 1 1 2 0 0 1 2 2 0 1 0 1 1 2 0 0 0 0 1 0 2 0 0 1 1 2 2 0 2 0]
Вы можете увидеть, что кластеризация немного похожа на классификацию в том плане, что каждый элемент получает метку. Однако нет никаких оснований утверждать, что данная метка является истинной и поэтому сами по себе метки не несут никакого априорного смысла. Давайте вернемся к примеру с кластеризацией изображений лиц, который мы обсуждали ранее. Возможно, что кластер 3, найденный с помощью алгоритма, содержит лишь лица вашего друга. Впрочем, вы можете узнать это только после того, как взгляните на фотографии, а само число 3 является произвольным. Единственная информация, которую дает вам алгоритм, - это то, что все лица, отнесенные к кластеру 3, схожи между собой.
В случае с кластеризацией, которую мы только что построили для двумерного синтетического набора данных, это означает, что мы не должны придавать значения тому факту, что одной группе был присвоен 0, а другой - 1. Повторный запуск алгоритма может привести к совершенно иной нумерации кластеров в силу случайного характера инициализации.
Ниже приводится новый график для тех же самых данных (рисунок 3). Центры кластеров записаны в атрибуте cluster_centers_ и мы наносим их на график в виде треугольников:
[In 51]: mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o') mglearn.discrete_scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2], markers='^', markeredgewidth=2)
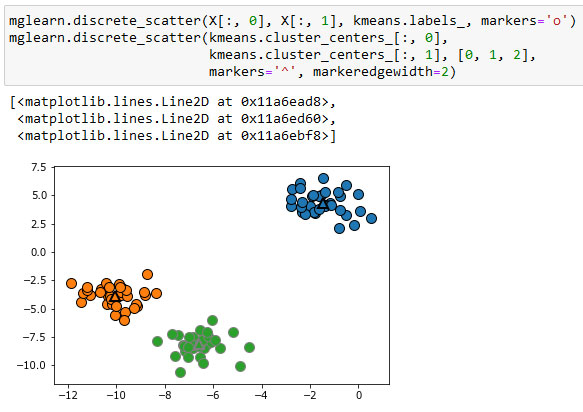
Рис.3. Принадлежность к кластерам и центры кластеров, найденные с помощью алгоритма k-средних, k=3
Кроме того, мы можем увеличить или уменьшить количество центров кластеров (рисунок 4):
[In 52]: fig, axes = plt.subplots(1, 2, figsize=(10, 5)) # использование двух центров кластеров: kmeans = KMeans(n_clusters=2) kmeans.fit(X) assignments = kmeans.labels_ mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[0]) # использование пяти центров кластеров: kmeans = KMeans(n_clusters=5) kmeans.fit(X) assignments = kmeans.labels_ mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[1])
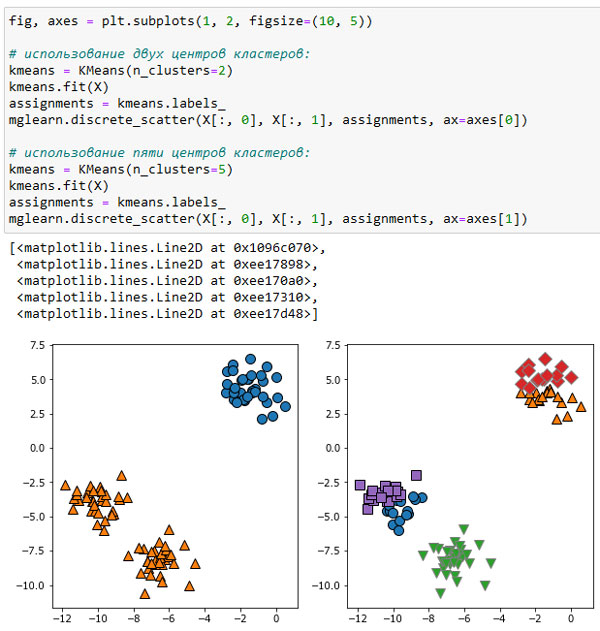
Рис.4. Принадлежность к кластерам, найденная с помощью алгоритма k-средних, k=3 (слева) и k=5 (справа)
На следующем шаге мы рассмотрим недостатки алгоритма k-средних.
