На этом шаге мы рассмотрим суть этого алгоритма.
Алгомеративная кластеризация (agglomerative clustering) относится к семейству алгоритмов кластеризации, в основе которых лежат одинаковые принципы: алгоритм начинает свою работу с того, что каждую точку данных заносит в свой собственный кластер и по мере выполнения объединяет два наиболее схожих между собой кластера до тех пор, пока не будет удовлетворен определенный критерии остановки. Критерий остановки, реализованный в scikit-learn - это количество кластеров, поэтому схожие между собой кластеры объединяются до тех пор, пока не останется заданное число кластеров. Есть несколько критериев связи (linkage), которые задают точный способ измерения "наиболее схожего кластера". В основе этих критериев лежит расстояние между двумя существующими кластерами.
В scikit-learn реализованы следующие три критерия:
- ward
- метод по умолчанию ward (метод Варда) выбирает и объединяет два кластера так, чтобы прирост дисперсии внутри кластеров был минимальным. Часто этот критерий приводит к
получению кластеров относительно одинакового размера.
- average
- метод average (метод средней связи) объединяет два кластера, которые имеют наименьшее среднее значение всех расстояний, измеренных между точками двух кластеров.
- complete
- метод complete (метод полной связи или метод максимальной связи) объединяет два кластера, которые имеют наименьшее расстояние между двумя их самыми удаленными точками.
ward подходит для большинства наборов данных и мы будем использовать именно его в наших примерах. Если кластеры имеют сильно различающиеся размеры (например, один кластер содержит намного больше точек данных, чем все остальные), использование критериев average или complete может дать лучший результат.
Следующий график (рисунок 1) иллюстрирует работу алгоритма агломеративной кластеризации на двумерном массиве данных, который ищет три кластера:
[In 60]:
mglearn.plots.plot_agglomerative_algorithm()
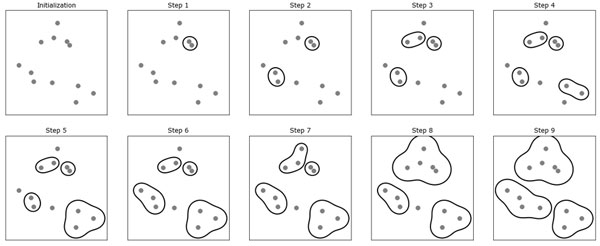
Рис.1. Алгоритм агломеративной кластеризации итеративно объединяет два ближайших кластера
Изначально количество кластеров равно количеству точек данных. Затем на каждом шаге объединяются два ближайших друг к другу кластера. На первых четырех шагах выбираются кластеры, состоящие из отдельных точек, и объединяются в кластеры, состоящие из двух точек. На шаге 5 один из 2-точечных кластеров вбирает в себя третью точку и т.д. На шаге 9 у нас остается три кластера. Поскольку мы установили количество кластеров равным 3, алгоритм останавливается.
Давайте рассмотрим работу алгоритма агломеративной кластеризации на простых трехкластерных данных, использованных здесь. Из-за своего способа работы алгоритм агломеративной кластеризации не может вычислить прогнозы для новых точек данных. Поэтому алгоритм агломеративной кластеризации не имеет метода predict(). Для того, чтобы построить модель и вычислить принадлежность к кластерам на обучающем наборе, используйте метод fit_predict().
Кроме того, мы могли бы воспользоваться атрибутом labels_, как мы это уже делали для алгоритма k-средних.
Результат показан на рисунке 2:
[In 61]: from sklearn.cluster import AgglomerativeClustering X, y = make_blobs(random_state=1) agg = AgglomerativeClustering(n_clusters=3) assignment = agg.fit_predict(X) mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment) plt.xlabel("Признак 0") plt.ylabel("Признак 1")
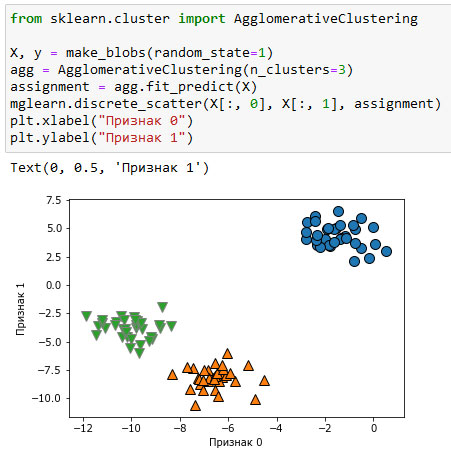
Рис.2. Принадлежность к кластерам, вычисленная алгоритмом агломеративной кластеризации с тремя кластерами
Как и ожидалось, алгоритм отлично восстанавливает кластеризацию. Хотя алгоритм агломеративной кластеризации, реализованный в scikit-learn, требует указать количество выделяемых кластеров, методы агломеративной кластеризации в некоторой степени помогают выбрать правильное количество кластеров, об этом и пойдет речь в следующих шагах.
На следующем шаге мы рассмотрим иерархическую кластеризацию и дендрограммы.
