На этом шаге мы рассмотрим, что из себя представляет векторное квантование.
Несмотря на то что алгоритм k-средних представляет собой алгоритм кластеризации, можно провести интересные параллели между алгоритмом k-средних и декомпозиционными методами типа PCA и NMF, которые мы обсуждали ранее. Возможно, вы помните, что РСА пытается найти направления максимальной дисперсии данных, в то время как NMF пытается найти аддитивные компоненты, которые часто соответствуют "экстремумам" или "группам" данных (см. рисунок 1 93 шага). Оба метода пытаются представить данные в виде суммы некоторых компонент. Алгоритм k-средних, напротив, пытается представить каждую точку данных в пространстве, используя центр кластера. Вообразите, что каждая точка представлена с помощью только одной компоненты, которая задается центром кластера. Рассмотрение алгоритма k-средних как декомпозиционного метода, в котором каждая точка представлена с помощью отдельной компоненты, называется векторным квантованием (vector quantization).
Давайте сравним PCA, NMF и алгоритм k-средних, показав выделенные компоненты (рисунок 1), а также реконструкции изображений лиц из тестового набора с использованием 100 компонент (рисунок 2). В алгоритме k-средних реконструкция изображения - это ближайший центр кластера, вычисленный на обучающем наборе:
[In 56]: X_train, X_test, y_train, y_test = train_test_split( X_people, y_people, stratify=y_people, random_state=0) nmf = NMF(n_components=100, random_state=0) nmf.fit(X_train) pca = PCA(n_components=100, random_state=0) pca.fit(X_train) kmeans = KMeans(n_clusters=100, random_state=0) kmeans.fit(X_train) X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test)) X_reconstructed_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)] X_reconstructed_nmf = np.dot(nmf.transform(X_test), nmf.components_)
[In 57]: fig, axes = plt.subplots(3, 5, figsize=(8, 8), subplot_kw={'xticks': (), 'yticks': ()}) fig.suptitle("Извлеченные компоненты") for ax, comp_kmeans, comp_pca, comp_nmf in zip( axes.T, kmeans.cluster_centers_, pca.components_, nmf.components_): ax[0].imshow(comp_kmeans.reshape(image_shape)) ax[1].imshow(comp_pca.reshape(image_shape), cmap='viridis') ax[2].imshow(comp_nmf.reshape(image_shape)) axes[0, 0].set_ylabel("k-средние") axes[1, 0].set_ylabel("pca") axes[2, 0].set_ylabel("nmf") fig, axes = plt.subplots(4, 5, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(8, 8)) fig.suptitle("Реконструкции") for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip( axes.T, X_test, X_reconstructed_kmeans, X_reconstructed_pca,X_reconstructed_nmf): ax[0].imshow(orig.reshape(image_shape)) ax[1].imshow(rec_kmeans.reshape(image_shape)) ax[2].imshow(rec_pca.reshape(image_shape)) ax[3].imshow(rec_nmf.reshape(image_shape)) axes[0, 0].set_ylabel("исходный вид") axes[1, 0].set_ylabel("k-средние") axes[2, 0].set_ylabel("pca") axes[3, 0].set_ylabel("nmf")
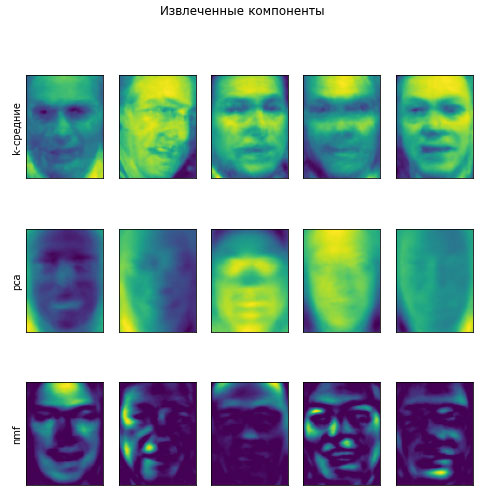
Рис.1. Сравнение центров кластеров, вычисленных с помощью алгоритма k-средних, и компонент, вычисленных с помощью PCA и NMF
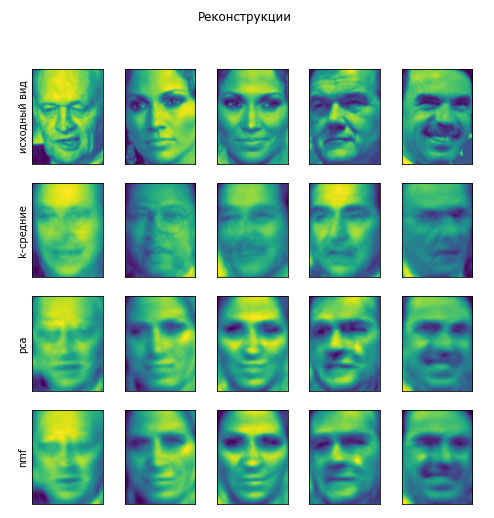
Рис.2. Сравнение реконструкций изображений, полученных с помощью алгоритма k-средних, PCA и NMF со 100 компонентами (или центрами
кластеров), алгоритм k-средних использует лишь один центр кластера на изображение
Интересная деталь векторного квантования с помощью алгоритма k-средних заключается в том, что для представления наших данных мы можем использовать число кластеров, намного превышающее число входных измерений. Давайте вернемся к данным two_moons. Применив к этим данным PCA или NMF, мы ничего примечательного с ними не сделаем, поскольку данные представлены двумя измерениями. Снижение до одного измерения с помощью PCA или NMF полностью бы разрушило структуру данных. Но мы можем найти более выразительное представление данных с помощью алгоритма k-средних, использовав большее количество центров кластеров (см. рисунок 3):
[In 58]: X, y = make_moons(n_samples=200, noise=0.05, random_state=0) kmeans = KMeans(n_clusters=10, random_state=0) kmeans.fit(X) y_pred = kmeans.predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=60, cmap='Paired') plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=60, marker='^', c=range(kmeans.n_clusters), linewidth=2, cmap='Paired') plt.xlabel("Признак 0") plt.ylabel("Признак 1") print("Принадлежность к кластерам:\n{}".format(y_pred)) Принадлежность к кластерам: [9 2 5 4 2 7 9 6 9 6 1 0 2 6 1 9 3 0 3 1 7 6 8 6 8 5 2 7 5 8 9 8 6 5 3 7 0 9 4 5 0 1 3 5 2 8 9 1 5 6 1 0 7 4 6 3 3 6 3 8 0 4 2 9 6 4 8 2 8 4 0 4 0 5 6 4 5 9 3 0 7 8 0 7 5 8 9 8 0 7 3 9 7 1 7 2 2 0 4 5 6 7 8 9 4 5 4 1 2 3 1 8 8 4 9 2 3 7 0 9 9 1 5 8 5 1 9 5 6 7 9 1 4 0 6 2 6 4 7 9 5 5 3 8 1 9 5 6 3 5 0 2 9 3 0 8 6 0 3 3 5 6 3 2 0 2 3 0 2 6 3 4 4 1 5 6 7 1 1 3 2 4 7 2 7 3 8 6 4 1 4 3 9 9 5 1 7 5 8 2]

Рис.3. Использование большого количества кластеров для выявления дисперсии в сложном наборе данных
Мы использовали 10 центров кластеров, это значит, что каждой точке данных теперь будет присвоен номер от 0 до 9. Мы можем убедиться в этом, поскольку данные теперь представлены с помощью 10 компонент (т.е. у нас теперь появилось 10 новых признаков), при этом все признаки равны 0, за исключением признака, который представляет собой центр кластера, назначенный конкретной точке данных. Применив это 10-мерное представление, теперь мы можем отделить эти два скопления данных в виде полумесяцев с помощью линейной модели, что было бы невозможным, если бы использовали два исходных признака. Кроме того, можно получить еще более выразительное представление данных, используя расстояния до каждого центра кластера в качестве признаков. Это можно сделать с помощью метода transform() класса kmeans:
[In 59]: distance_features = kmeans.transform(X) print("Форма характеристик-расстояний: {}".format(distance_features.shape)) print("Характеристики-расстояния:\n{}".format(distance_features)) Форма характеристик-расстояний: (200, 10) Характеристики-расстояния: [[0.9220768 1.46553151 1.13956805 ... 1.16559918 1.03852189 0.23340263] [1.14159679 2.51721597 0.1199124 ... 0.70700803 2.20414144 0.98271691] [0.78786246 0.77354687 1.74914157 ... 1.97061341 0.71561277 0.94399739] ... [0.44639122 1.10631579 1.48991975 ... 1.79125448 1.03195812 0.81205971] [1.38951924 0.79790385 1.98056306 ... 1.97788956 0.23892095 1.05774337] [1.14920754 2.4536383 0.04506731 ... 0.57163262 2.11331394 0.88166689]]
Алгоритм k-средних является очень популярным алгоритмом кластеризации не только потому, что его относительно легко понять и реализовать, но и потому, что он работает сравнительно быстро. Алгоритм k-средних легко масштабируется на большие наборы данных, а scikit-learn еще и включает в себя более масштабируемый вариант, реализованный в классе MiniBatchKMeans, который может обрабатывать очень большие наборы данных.
Один из недостатков алгоритма k-средних заключается в том, что он зависит от случайной инициализации (т.е. результат алгоритма зависит от случайного стартового значения). По умолчанию scikit-learn запускает алгоритм 10 раз с 10 различными случайными стартовыми значениями и возвращает лучший результат. Дополнительными недостатками алгоритма k-средних являются относительно строгие предположения о форме кластеров, а также необходимость задать число выделяемых кластеров (которое в реальной практике может быть неизвестно).
Далее мы рассмотрим еще два алгоритма кластеризации, которые в некотором роде позволяют исправить вышеописанные недостатки.
На следующем шаге мы рассмотрим агломеративную кластеризацию.
