На этом шаге мы рассмотрим результаты использования этого алгоритма, примененного к анализу лиц.
Теперь давайте посмотрим на результаты агломеративной кластеризации:
[In 81]: # извлекаем кластеры с помощью агломеративной кластеризации по методу Варда agglomerative = AgglomerativeClustering(n_clusters=10) labels_agg = agglomerative.fit_predict(X_pca) print("Размеры кластеров для агломеративной кластеризации: {}".format( np.bincount(labels_agg))) Размеры кластеров для агломеративной кластеризации: [478 254 317 119 96 191 424 17 55 112]
Видно, что алгоритм агломеративной кластеризации распределил данные по кластерам, размер которых варьирует от 17 до 478 изображений. В отличие от алгоритма k-средних размеры кластеров варьируют сильнее, но при этом значительно меньше, если сравнивать их с размерами кластеров, полученными с помощью алгоритма DBSCAN.
Мы можем вычислить ARI, чтобы оценить сходство результатов, полученных с помощью агломеративной кластеризации и кластеризации k-средних:
[In 82]: print("ARI: {:.2f}".format(adjusted_rand_score(labels_agg, labels_km))) ARI: 0.07
Значение ARI, равное всего лишь 0.07, означает, что кластеризации labels_agg и labels_km имеют мало общего между собой. Это неудивительно, учитывая тот факт, что в алгоритме k-средних точки, удаленные от центров кластеров, по-видимому, имеют мало общего между собой.
Далее мы можем построить дендрограммы (рисунок 1). Мы ограничим глубину дерева, поскольку ветвление по 2063 отдельным точкам данных приведет к построению нечитаемоего очень плотного графика:
[In 83]: linkage_array = ward(X_pca) # строим дендрограмму для linkage_array # содержащего расстояния между кластерами plt.figure(figsize=(20, 5)) dendrogram(linkage_array, p=7, truncate_mode='level', no_labels=True) plt.xlabel("Индекс примера") plt.ylabel("Кластерное расстояние")
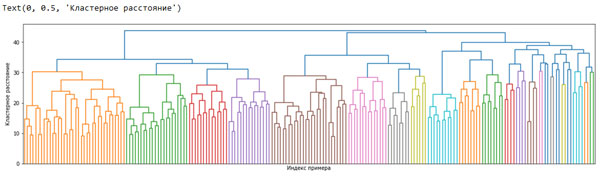
Рис.1. Дендрограмма агломеративной кластеризации для набора изображений лиц
Построив 10 кластеров, мы срезаем дерево в самой верхней части, в которой расположены 10 вертикальных линий. На дендрограмме, построенной для синтетических данных (рисунок 2 102 шага), вы, проанализировав длину ветвей, могли прийти к выводу, что два или три кластера могут описать данные надлежащим образом. Что касается набора изображений лиц, здесь, по-видимому, не будет какого-то очевидного числа. Некоторые ветви представляют собой более четко обособленные группы, но, по-видимому, это никак не связано с оптимальным количеством кластеров. Это неудивительно, учитывая результаты алгоритма DBSCAN, который попытался сгруппировать все кластеры вместе.
Давайте визуализируем эти 10 кластеров, как мы это делали ранее для алгоритма k-средних (рисунок 2). Обратите внимание, что в агломеративной кластеризации не существует такого понятия, как центр кластера (хотя мы могли бы вычислить среднее значение) и мы просто показываем первые несколько точек в каждом кластере. Кроме того, мы покажем количество точек в каждом кластере, выведя его слева от первого изображения каждого ряда:
[In 84]: n_clusters = 10 for cluster in range(n_clusters): mask = labels_agg == cluster fig, axes = plt.subplots(1, 10, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(15, 8)) axes[0].set_ylabel(np.sum(mask)) for image, label, asdf, ax in zip(X_people[mask], y_people[mask], labels_agg[mask], axes): ax.imshow(image.reshape(image_shape), vmin=0, vmax=1) ax.set_title(people.target_names[label].split()[-1], fontdict={'fontsize': 9})

Рис.2. Изображения, случайно выбранные из кластеров с помощью вышеприведенного программного кода (каждый ряд соответствует одному кластеру, число слева указывает количество изображений в каждом кластере)
Хотя некоторые кластеры, похоже, имеют содержательную интерпретацию, многие из них слишком велики, чтобы быть на самом деле однородными. Чтобы получить более однородные кластеры, мы можем запустить алгоритм снова, на этот раз с 40 кластерами, и выбрать некоторые особо интересные кластеры (рисунок 3):
# извлекаем кластеры с помощью агломеративной кластеризации по методу Варда [In 85]: agglomerative = AgglomerativeClustering(n_clusters=40) labels_agg = agglomerative.fit_predict(X_pca) print("размеры кластеров для аглом. кластеризации: {}".format(np.bincount(labels_agg))) n_clusters = 40 for cluster in [10, 13, 19, 22, 36]: # вручную выбранные "интересные" кластеры mask = labels_agg == cluster fig, axes = plt.subplots(1, 15, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(15, 8)) cluster_size = np.sum(mask) axes[0].set_ylabel("#{}: {}".format(cluster, cluster_size)) for image, label, asdf, ax in zip(X_people[mask], y_people[mask], labels_agg[mask], axes): ax.imshow(image.reshape(image_shape), vmin=0, vmax=1) ax.set_title(people.target_names[label].split()[-1], fontdict={'fontsize': 9}) for i in range(cluster_size, 15): axes[i].set_visible(False) размеры кластеров для аглом. кластеризации: [ 72 116 52 101 189 121 44 2 155 24 34 30 29 22 6 71 54 131 41 53 20 96 30 36 12 61 54 8 182 19 7 17 50 5 22 22 35 11 27 2]

Рис.3. Изображения из отобранных кластеров, которые были найдены алгоритмом агломеративной кластеризации (количество кластеров равно 40), текста слева показывает индекс кластера и общее количество точек в кластере
В данном случае кластеризация, похоже, выделила "улыбчивых чернокожих", "любителей рубашек с воротником" и "Уильямсов". Кроме того, мы могли бы найти аналогичные кластеры с помощью дендрограммы, если бы проводили более детальный анализ.
Архив блокнота со всеми вычислениями, выполненными на 82-110 шагах, можно взять здесь.
На следующем шаге мы сделаем выводы по методам кластеризации.
