На этом шаге мы рассмотрим результаты работы этого алгоритма для кластеризации лиц.
Мы увидели, что с помощью алгоритма DBSCAN невозможно получить больше одного большого кластера. Алгоритмы агломеративной кластеризации и k-средних имеют гораздо больше шансов сформировать кластеры одинакового размера, но нам задать нужное количество кластеров. Мы могли бы задать количество кластеров равным известному количеству людей в наборе данных, хотя очень маловероятно, что алгоритм неконтролируемой кластеризации сможет восстановить их. Вместо этого мы можем начать с небольшого количества кластеров (например, с 10), которое, возможно, позволит нам проанализировать каждый кластер:
[In 78]: # извлекаем кластеры с помощью k-средних km = KMeans(n_clusters=10, random_state=0) labels_km = km.fit_predict(X_pca) print("Размеры кластеров k-средние: {}".format(np.bincount(labels_km))) Размеры кластеров k-средние: [113 256 188 147 216 180 258 211 139 355]
Видно, что алгоритм кластеризации k-средних распределил данные по кластерам, размер которых варьирует от 113 до 355 изображений. Это сильно отличается от результата алгоритма DBSCAN.
Далее мы можем проанализировать результаты алгоритма k-средних, визуализировав центры кластеров (рисунок 1). Поскольку мы кластеризировали данные, полученные с помощью PCA, нам нужно повернуть центры кластеров обратно в исходное пространство, чтобы визуализировать их, используя pca.inverse_transform():
[In 79]: fig, axes = plt.subplots(2, 5, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(12, 4)) for center, ax in zip(km.cluster_centers_, axes.ravel()): ax.imshow(pca.inverse_transform(center).reshape(image_shape), vmin=0, vmax=1)
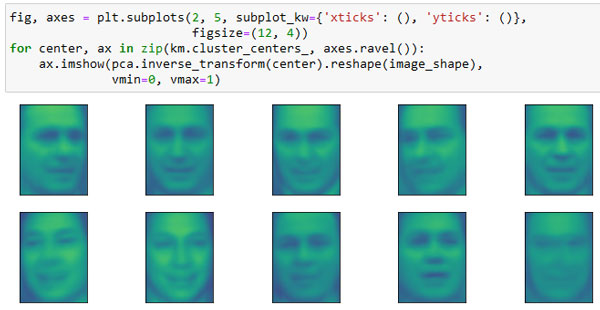
Рис.1. Центры кластеров, найденные с помощью k-средних, количество кластеров равно 10
Центры кластеров, найденные с помощью алгоритма k-средних, представляют собой сильно сглаженные лица. Это неудивительно, учитывая, что каждый центр - это усредненное изображение лиц, попавших в кластер. Использование уменьшенного с помощью PCA представления данных усиливает сглаженность изображений (сравните с реконструкциями лиц на рисунке 2 91 шага, когда использовалось 100 компонент). Похоже, что кластеризация выделила разные повороты лиц, разные выражения лиц (кажется, третий центр кластера показывает улыбающееся лицо), а также наличие воротника у рубашки.
Для более детального просмотра на рисунке 2 мы выведем для каждого центра кластера пять наиболее типичных изображений в кластере (изображения, присвоенные кластеру и находящиеся ближе всего к центру кластера) и пять самых нетипичных изображений в кластере (изображения, присвоенные кластеру и находящиеся дальше всего от центра кластера):
[In 80]:
mglearn.plots.plot_kmeans_faces(km, pca, X_pca, X_people,
y_people, people.target_names)
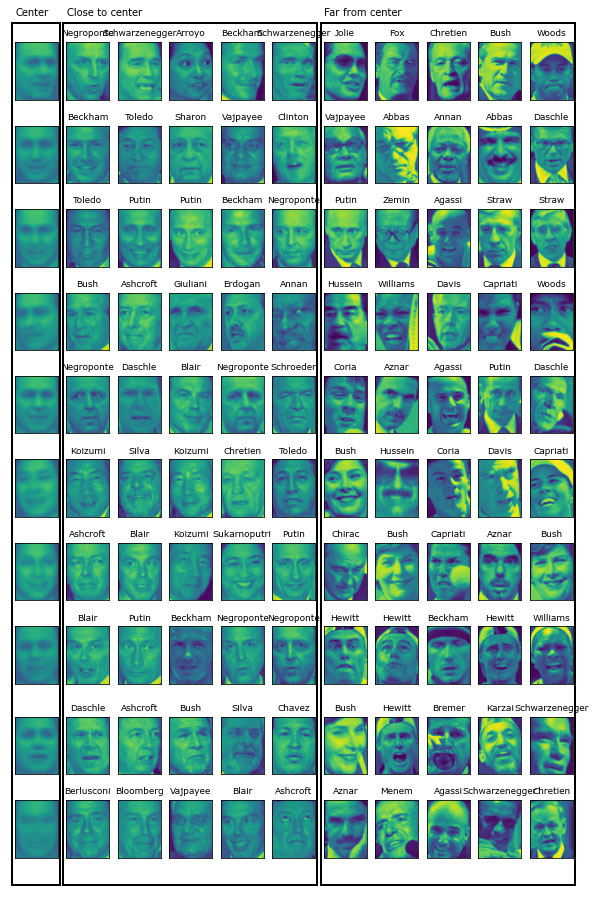
Рис.2. Примеры изображений для каждого кластера, найденного с помощью алгоритма k-средних - центры кластеров находятся слева, затем следуют пять точек,
максимально близко расположенных к центру кластера, и пять точек, максимально удаленных от центра кластера
Рисунок 2 подтверждает наш вывод об улыбающих лицах в третьем кластере и важности поворота лица для других кластеров. Однако "нетипичные" точки сильно отличаются от центров кластеров и их назначение кластеру кажется несколько произвольным. Это может быть обусловлено тем фактом, что алгоритм k-средних разбивает все точки данных на группы и в отличие от алгоритма DBSCAN в нем отсутствует понятие "шумовая точка". При использовании большего количества кластеров алгоритм сможет найти более тонкие различия. Однако увеличения числа кластеров сделает ручной анализ еще более трудоемким.
На следующем шаге мы рассмотрим анализ набора изображений лиц с помошью алгоритма агломеративной кластеризации.
