На этом шаге мы рассмотрим использование полиномов исходных признаков.
Использование биннинга - это способ увеличения пространства входных признаков. Еще один способ заключается в использовании полиномов (polynomials) исходных признаков. Для признака х мы рассмотрим х ** 2, х ** 3, х ** 4 и так далее. Данную операцию можно выполнить с помощью PolynomialFeatures модуля preprocessing:
[In 21]: from sklearn.preprocessing import PolynomialFeatures # задаем степень полинома 10: # значение по умолчанию "include_bias=True" добавляет признак-константу 1 poly = PolynomialFeatures(degree=10, include_bias=False) poly.fit(X) X_poly = poly.transform(X)
Использование 10-й степени дает 10 признаков:
[In 22]: print("форма массива X_poly: {}".format(X_poly.shape)) форма массива X_poly: (100, 10)
Давайте сравним элементы массива X_poly с элементами массива X:
[In 23]: print("Элементы массива X:\n{}".format(X[:5])) print("Элементы массива X_poly:\n{}".format(X_poly[:5])) Элементы массива X: [[-0.75275929] [ 2.70428584] [ 1.39196365] [ 0.59195091] [-2.06388816]] Элементы массива X_poly: [[-7.52759287e-01 5.66646544e-01 -4.26548448e-01 3.21088306e-01 -2.41702204e-01 1.81943579e-01 -1.36959719e-01 1.03097700e-01 -7.76077513e-02 5.84199555e-02] [ 2.70428584e+00 7.31316190e+00 1.97768801e+01 5.34823369e+01 1.44631526e+02 3.91124988e+02 1.05771377e+03 2.86036036e+03 7.73523202e+03 2.09182784e+04] [ 1.39196365e+00 1.93756281e+00 2.69701700e+00 3.75414962e+00 5.22563982e+00 7.27390068e+00 1.01250053e+01 1.40936394e+01 1.96178338e+01 2.73073115e+01] [ 5.91950905e-01 3.50405874e-01 2.07423074e-01 1.22784277e-01 7.26822637e-02 4.30243318e-02 2.54682921e-02 1.50759786e-02 8.92423917e-03 5.28271146e-03] [-2.06388816e+00 4.25963433e+00 -8.79140884e+00 1.81444846e+01 -3.74481869e+01 7.72888694e+01 -1.59515582e+02 3.29222321e+02 -6.79478050e+02 1.40236670e+03]]
Вы можете понять содержательный смысл этих признаков, вызвав метод get_feature_names(), который выведет название каждого признака:
[In 24]: print("Имена полиномиальных признаков:\n{}".format(poly.get_feature_names())) Имена полиномиальных признаков: ['x0', 'x0^2', 'x0^3', 'x0^4', 'x0^5', 'x0^6', 'x0^7', 'x0^8', 'x0^9', 'x0^10']
Видно, что первый столбец X_poly точно соответствует X, в то время как другие столбцы являются различными степенями первого элемента.
Использование полиномиальных признаков в модели линейной регрессии дает классическую модель полиномиальной регрессии (polynomial regression), представленную на рисунке 1:
[In 25]: reg = LinearRegression().fit(X_poly, y) line_poly = poly.transform(line) plt.plot(line, reg.predict(line_poly), label='полиномиальная линейная регрессия') plt.plot(X[:, 0], y, 'o', c='k') plt.ylabel("Выход регрессии") plt.xlabel("Входной признак") plt.legend(loc="best")
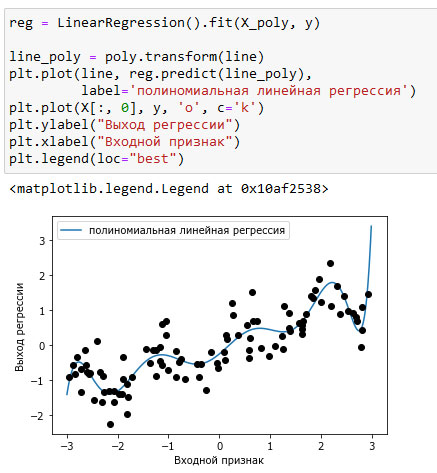
Рис.1. Полиномиальная линейная регрессия, использовался полином 10-й степени
Видно, что на этом одномерном наборе данных полиномиальные признаки дают очень сглаженную подгонку. Однако полиномы высокой степени, как правило, резко меняют направление на границах области определения или в менее плотных областях данных.
Для сравнения ниже приводится модель ядерного SVM, обученная на исходных данных без каких-либо преобразований (см. рисунок 2):
[In 26]: from sklearn.svm import SVR for gamma in [1, 10]: svr = SVR(gamma=gamma).fit(X, y) plt.plot(line, svr.predict(line), label='SVR gamma={}'.format(gamma)) plt.plot(X[:, 0], y, 'o', c='k') plt.ylabel("Выход регрессии") plt.xlabel("Входной признак") plt.legend(loc="best")
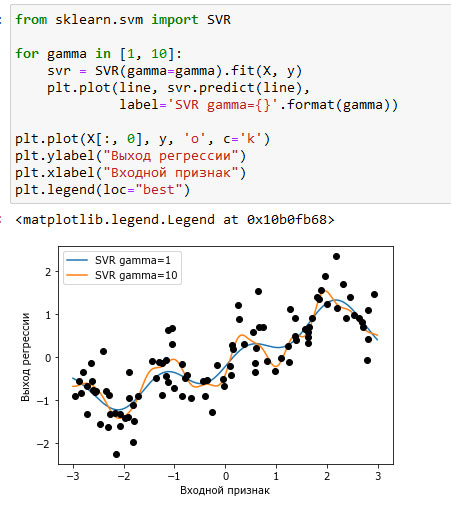
Рис.2. Сравнение различных параметров gamma для SVM c RBF-ядром
Используя более сложную модель, модель ядерного SVM, мы можем получить такой же сложный прогноз, как в случае полиномиальной регрессии, не прибегая к явному преобразованию признаков.
На следующем шаге мы закончим изучение этого вопроса.
