На этом шаге мы рассмотрим, как можно учесть экспертные знания.
Широко распространенный способ хранения дат на компьютерах - использование POSIX-времени, которое представляет собой количество секунд, прошедших с полуночи (00:00:00) 1 января 1970 года (оно же является точкой отсчета Unix-времени). В качестве первой попытки мы можем воспользоваться им для нашего представления дат:
[In 52]: # извлекаем значения зависимой переменной (количество велосипедов, взятых в прокат) y = citibike.values # преобразуем время в формат POSIX с помощью "%s" X = citibike.index.astype("int64").values.reshape(-1, 1) // 10**9
Сначала мы зададим функцию, чтобы разбить данные на обучающий и тестовый наборы, построим модель и визуализируем результат:
[In 53]: # используем первые 184 точки данных для обучения, а остальные для тестирования n_train = 184 # функция, которая строит модель на данном наборе признаков и визуализирует ее def eval_on_features(features, target, regressor): # разбиваем массив признаков на обучающую и тестовую выборки X_train, X_test = features[:n_train], features[n_train:] # также разбиваем массив с зависимой переменной y_train, y_test = target[:n_train], target[n_train:] regressor.fit(X_train, y_train) print("R^2 для тестового набора: {:.2f}".format(regressor.score(X_test, y_test))) y_pred = regressor.predict(X_test) y_pred_train = regressor.predict(X_train) plt.figure(figsize=(10, 3)) plt.xticks(range(0, len(X), 8), xticks.strftime("%a %m-%d"), rotation=90, ha="left") plt.plot(range(n_train), y_train, label="обуч") plt.plot(range(n_train, len(y_test) + n_train), y_test, '-', label="тест") plt.plot(range(n_train), y_pred_train, '--', label="прогноз обуч") plt.plot(range(n_train, len(y_test) + n_train), y_pred, '--', label="прогноз тест") plt.legend(loc=(1.01, 0)) plt.xlabel("Дата") plt.ylabel("Частота проката")
Ранее мы уже видели, что случайный лес требует очень незначительной предварительной обработки данных, что, по-видимому, делает его оптимальной моделью для старта. Мы передаем функции eval_on_features() массив с признаком X (даты, преобразованные в POSIX-формат), y и модель случайного леса. Рисунок 1 показывает результат:
[In 54]: from sklearn.ensemble import RandomForestRegressor regressor = RandomForestRegressor(n_estimators=100, random_state=0) plt.figure() eval_on_features(X, y, regressor) R^2 для тестового набора: -0.09
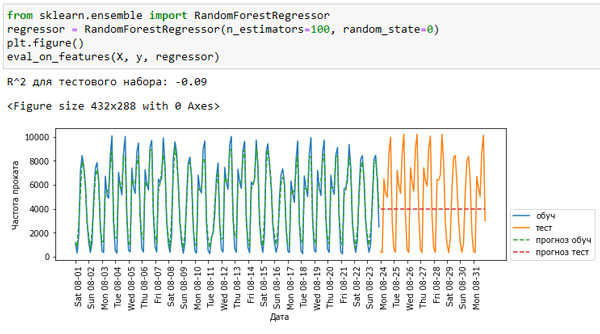
Рис.1. Прогнозы, вычисленные случайным лесом (использовались даты, пребразованные в формат времени POSIX)
Как это обычно бывает при построении случайного леса, правильность прогнозов на обучающем наборе получилась довольно высокой. Однако для тестового набора прогнозируется ровная линия. Значение R2 равно -0.09, это означает, что наша модель ничему не научилась. Что произошло?
Проблема обусловлена сочетанием типа нашего признака и используемого метода (в данном случае случайного леса). Значения признака на основе POSIX-времени для тестового набора находятся вне диапазона значений этого признака в обучающей выборке: точки тестового набора в отличие от точек обучающего набора имеют более поздние временные метки. Дерево, а следовательно и случайный лес, не могут экстраполировать (extrapolate) значения признаков, лежащие вне диапазона значений обучающих данных. Итог - модель просто предсказывает значение зависимом переменной для ближайшем точки обучающего набора (для последней временной метки, которую она запомнила).
Ясно, что мы можем улучшить прогноз. Это тот момент, когда на помощь приходят наши "экспертные знания". Взглянув на то, как меняется частота проката в обучающих данных, можно выделить два очень важных фактора: время суток и день недели. Итак, давайте добавим эти два признака. Мы не смогли построить модель, используя время в формате POSIX, поэтому мы отбрасываем этот признак. Для начала давайте попробуем время суток. Как показывает рисунок 2, теперь прогнозы имеют одинаковую структуру для каждого дня недели:
[In 55]: X_hour = citibike.index.hour.values.reshape(-1, 1) eval_on_features(X_hour, y, regressor) R^2 для тестового набора: 0.85
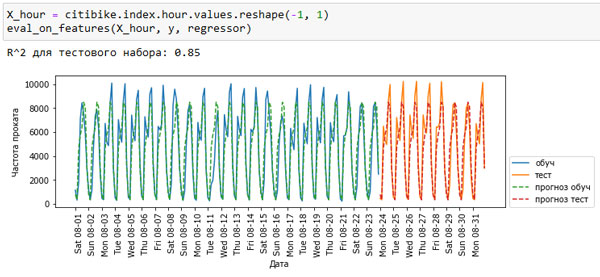
Рис.2. Прогнозы, вычисленные случайным лесом (использовалось время суток)
Значение R2 стало уже намного лучше, но прогнозы явно не учитывают эффект, обусловленный днем недели. Теперь давайте еще добавим день недели (см. рисунок 3):
[In 56]: X_hour_week = np.hstack([citibike.index.dayofweek.values.reshape(-1, 1), citibike.index.hour.values.reshape(-1, 1)]) eval_on_features(X_hour_week, y, regressor) R^2 для тестового набора: 0.98
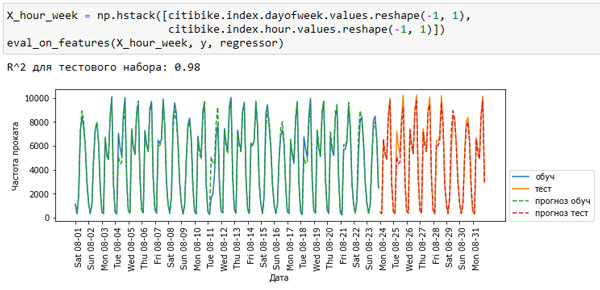
Рис.3. Прогнозы, вычисленные случайным лесом (использовались день недели и время суток)
На следующем шаге мы закончим изучение этого вопроса.
