На этом шаге мы воспользуемся еще одной моделью для получения аналогичного результата.
Теперь у нас есть модель, которая отражает периодичность поведения, учитывая день недели и время суток. Она имеет значение R2, равное 0.98, и демонстрирует довольно хорошую прогностическую способность. Модель научилась прогнозировать среднее количество арендованных велосипедов для каждой комбинации дня недели и времени суток на основе выборки, включающей первые 23 дня августа. На самом деле эта задача не требует такой сложной модели, как случайный лес, поэтому давайте попробуем более простую модель, например, LinearRegression (см. рисунок 1):
[In 57]: from sklearn.linear_model import LinearRegression eval_on_features(X_hour_week, y, LinearRegression()) R^2 для тестового набора: 0.33
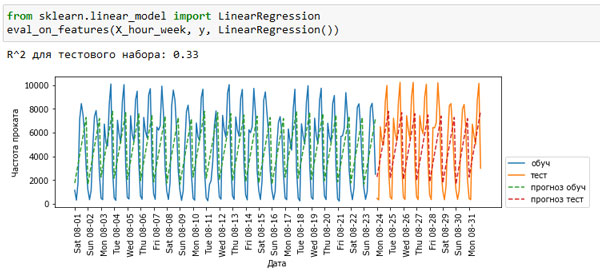
Рис.1. Прогнозы, вычисленные линейной регрессией (использовались день недели и время суток)
LinearRegression работает гораздо хуже, а периодическая структура данных выглядит странно. Причиной этого является тот факт, что мы закодировали день недели и время суток с помощью целочисленных значении и теперь эти характеристики интерпретируются как непрерывные переменные. В силу этого линейная модель может построить лишь линейную функцию от времени суток - в более позднее время суток наблюдается большее количество арендованных велосипедов. Однако структура данных сложнее, чем предполагает модель. Мы можем учесть это, преобразовав признаки, закодированные целыми числами, в дамми-переменные с помощью OneHotEncoder() (см. рисунок 2):
[In 58]: enc = OneHotEncoder() X_hour_week_onehot = enc.fit_transform(X_hour_week).toarray()
[In 59]:
eval_on_features(X_hour_week_onehot, y, Ridge())
R^2 для тестового набора: 0.87
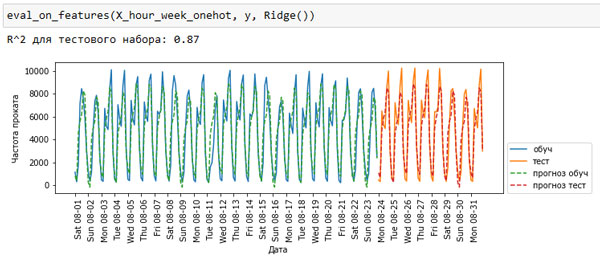
Рис.2. Прогнозы, вычисленные линейной регрессией (использовалось прямое кодирование времени суток и дня недели)
Данная процедура дает гораздо лучший результат в отличие от кодирования наших признаков в виде непрерывных переменных. Теперь линейная модель вычисляет один коэффициент для каждого дня недели и один коэффициент для каждого времени суток. Тем не менее, это означает, что паттерн "времени суток" распределяется по всем дням недели.
Используя взаимодействия, мы можем вычислить коэффициент для каждой комбинации дня недели и времени суток (см. рисунок 3):
[In 60]: poly_transformer = PolynomialFeatures(degree=1, interaction_only=True, include_bias=False) X_hour_week_onehot_poly = poly_transformer.fit_transform(X_hour_week_onehot) lr = Ridge() eval_on_features(X_hour_week_onehot_poly, y, lr) R^2 для тестового набора: 0.97
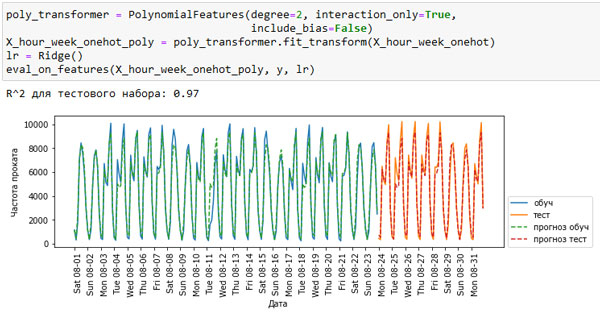
Рис.3. Прогнозы, вычисленные линейной регрессией (использовались взаимодействия дня недели и времени суток)
Наконец, это преобразование дает модель, которая обладает такой же высокой прогностической способностью, что и случайный лес. Большим преимуществом данной модели является ее понятность: мы вычисляем по одному коэффициенту для каждой комбинации дня недели и времени суток. Мы можем просто построить график коэффициентов, вычисленных с помощью модели, что было бы невозможно для случайного леса.
Во-первых, мы создаем имена для наших признаков:
[In 61]: hour = ["%02d:00" % i for i in range(0, 24, 3)] day = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"] features = day + hour
Затем мы присваиваем имена всем взаимодействиям, извлеченным с помощью PolynomialFeatures, используя метод get_feature_names(), и сохраняем лишь те признаки, у которых коэффициенты отличны от нуля:
[In 62]: features_poly = poly_transformer.get_feature_names(features) features_nonzero = np.array(features_poly)[lr.coef_ != 0] coef_nonzero = lr.coef_[lr.coef_ != 0]
Теперь мы можем визуализировать коэффициенты, извлеченные с линейной модели (показаны на рис. 4):
plt.figure(figsize=(15, 2)) plt.plot(coef_nonzero, 'o') plt.xticks(np.arange(len(coef_nonzero)), features_nonzero, rotation=90) plt.xlabel("Оценка коэффициента") plt.ylabel("Признак")
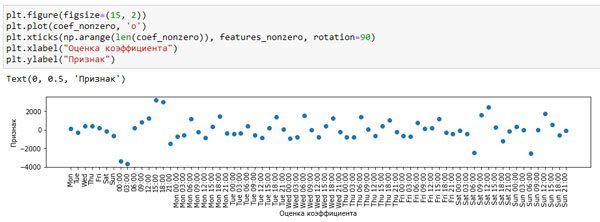
Рис.4. Коэффициенты линейной регрессии (использовались взаимодействия дня недели и времени суток) (изображение кликабельно)
Архив блокнота со всеми вычислениями, выполненными на 116-130 шагах, и файлом с исходными данными можно взять здесь.
На следующем шаге мы рассмотрим выводы и перспективы.
