На этом шаге мы рассмотрим назначение и использование этих параметров.
Есть еще несколько способов подытожить информацию матрицы ошибок, наиболее часто используемыми из них являются точность и полнота. Точность (precision) показывает, сколько из предсказанных положительных примеров оказались действительно положительными. Таким образом, точность - это доля истинно положительных примеров от общего количества предсказанных положительных примеров.
Точность используется в качестве показателя качества модели, когда цель состоит в том, чтобы снизить количество ложно положительных примеров. В качестве примера представьте модель, которая дожна спрогнозировать, будет ли эффективен новый лекарственный препарат при лечении болезни. Клинические испытания, как известно, дороги, и фармацевтическая компания хочет провести их лишь в том случае, когда полностью убедится, что препарат действительно работает. Поэтому важно минимизировать количество ложно положительных примеров, другими словами, необходимо увеличить точность. Точность также известна как прогностическая ценность положительного результата (positive predictive value, PPV).
С другой стороны, полнота (recall) показывает, сколько от общего числа фактических положительных примеров было предсказано как положительный класс. Полнота - это доля истинно положительных примеров от общего количества фактических положительных примеров.
Полнота используется в качестве показателя качества модели, когда нам необходимо определить все положительные примеры, то есть, когда важно снизить количество ложно отрицательных примеров. Пример диагностики рака, приведенный ранее в этой главе, является хорошей иллюстрацией подобной задачи: важно выявить всех больных пациентов, при этом, возможно, включив в их число здоровых пациентов. Другие названия полноты - чувствительность (sensitivity), процент результативный ответов или хит-рейт (hit rate) и доля истинно положительных примеров (true positive rate, TPR).
Всегда необходимо найти компромисс между оптимизацией полноты и оптимизацией точности. Вы легко можете получить идеальную полноту, спрогнозировав все примеры как положительные - не будет никаких ложно отрицательных и истинно отрицательных примеров. Однако прогнозирование всех примеров как положительных приведет к большому количеству ложно положительных примеров, и, следовательно, точность будет очень низкой. С другой стороны, допустим, у вас есть набор данных из 201 примера и вы строите модель, которая прогнозирует один пример как положительный (и этот пример действительно относится к положительному классу), а все остальные примеры относит к отрицательному классу. Предположим, матрица ошибок выглядит следующим образом.
| TN 100 примеров |
FP 0 примеров |
| FN 100 примеров |
TP 1 пример |
Вычисляем точность и полноту. Точность будет идеальной, а полнота - очень низкой.
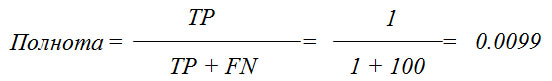
Точность и полнота - это лишь две метрики из множества показателей классификации, получаемых с помощью TP, FP, TN и FN. Вы можете найти подробное описание метрик в
Википедии. Среди специалистов по машинному обучению точность и полнота являются, возможно, наиболее
часто используемыми метриками бинарной классификации, однако остальные специалисты могут использовать другие связанные с ними показатели.
Хотя точность и полнота являются очень важными метриками, сами по себе они не дадут вам полной картины. Одним из способов подытожить их является F-мера (F-measure), которая представляет собой гармоническое среднее точности и полноты:
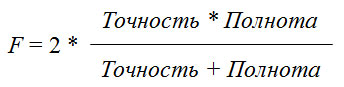
Этот вариант вычисления F-меры еще известен как f1-мера. Поскольку f1-мера учитывает точность и полноту, то для бинарной классификации несбалансированных данных она может быть более лучшей метрикой, чем правильность. Давайте применим ее к прогнозам для нашего набора данных "девятка против остальных", полученным нами ранее. В данном случае мы будем считать класс "девятка" положительным классом (он получает метку True, тогда как класс "не-девятка" получает метку False), таким образом, положительный класс является миноритарным классом:
[In 47]: from sklearn.metrics import f1_score print("f1-мера наибольшая частота: {:.2f}".format( f1_score(y_test, pred_most_frequent))) print("f1-мера дамми: {:.2f}".format(f1_score(y_test, pred_dummy))) print("f1-мера дерево: {:.2f}".format(f1_score(y_test, pred_tree))) print("f1-мера логистическая регрессия: {:.2f}".format( f1_score(y_test, pred_logreg))) f1-мера наибольшая частота: 0.00 f1-мера дамми: 0.00 f1-мера дерево: 0.55 f1-мера логистическая регрессия: 0.92
Здесь мы можем отметить два момента. Во-первых, мы получаем сообщение об ошибке для прогнозов модели most_frequent, поскольку не было получено ни одного прогноза положительного класса (таким образом, знаменатель в формуле расчета f1-меры равен нулю). Кроме того, мы можем увидеть довольно сильное различие между прогнозами дамми-модели и прогнозами дерева, которое не так явно бросается в глаза, когда мы анализируем только правильность. Использовав f1-меру для оценки качества, мы снова подытоживаем прогностическую способность с помощью одного числа. Однако, похоже, что f1-мера действительно дает более лучшее представление о качестве модели, чем правильность. Вместе с тем недостаток f1-меры заключается в том, что в отличие от правильности ее труднее интерпретировать и объяснить.
Если мы хотим получить более развернутый отчет о точности, полноте и f1-мере, можно воспользоваться удобной функцией classification_report(), чтобы вычислить все три метрики сразу и распечатать их в привлекательном виде:
[In 48]: from sklearn.metrics import classification_report print(classification_report(y_test, pred_most_frequent, target_names=["not nine", "nine"])) precision recall f1-score support not nine 0.90 1.00 0.94 403 nine 0.00 0.00 0.00 47 accuracy 0.90 450 macro avg 0.45 0.50 0.47 450 weighted avg 0.80 0.90 0.85 450
Функция classification_report() печатает отчет, в котором выводятся показатели точности, полноты и f1-меры для отрицательного и положительного классов. Миноритарный класс "девятка" считается положительным классом. Значение f1-меры для него равно 0. Для мажоритарного класса "не-девятка" значение f1-меры равно 0.94. Кроме того, полнота для класса "не-девятка" равна 1, поскольку мы классифицировали все примеры как "не-девятки". Крайний правый столбец - это поддержка (support), которая равна фактическому количеству примеров данного класса.
В последней строке отчета приводятся средние значения метрик, взвешенные по количеству фактических примеров в каждом классе. Поясним процесс вычисления взвешенного среднего значения для примере f1-метрики. Сначала вычисляем веса отрицательного и положительного классов. Вес отрицательного класса равен 403/450=0.90. Вес положительного класса равен 47/450=0.10. Теперь спрогнозированное значение f1-меры для каждого класса умножаем на вес соответствующего класса, складываем результаты и получаем взвешенное среднее значение f1-меры: 0.90 * 0.94 + 0.10 * 0.00 = 0.85. Ниже даны еще два отчета - для дамми-классификатора и логстической регрессии:
[In 49]: print(classification_report(y_test, pred_dummy, target_names=["not nine", "nine"])) precision recall f1-score support not nine 0.90 1.00 0.94 403 nine 0.00 0.00 0.00 47 accuracy 0.90 450 macro avg 0.45 0.50 0.47 450 weighted avg 0.80 0.90 0.85 450
[In 50]: print(classification_report(y_test, pred_logreg, target_names=["not nine", "nine"])) precision recall f1-score support not nine 0.99 1.00 0.99 403 nine 0.98 0.87 0.92 47 accuracy 0.98 450 macro avg 0.98 0.93 0.96 450 weighted avg 0.98 0.98 0.98 450
Взглянув на отчеты, можно заметить, что различия между дамми-моделью и моделью логистической регрессии уже не столь очевидны. Решение о том, какой класс объявить положительным, имеет большое влияние на метрики. Несмотря на то, что в дамми-классификаторе f1-мера для класса "девятка" равна 0.13 (в сравнении с 0.89 для логистической регрессии), а для класса "не-девятка" она равна 0.90 (в сравнении с 0.99 для логистической регрессии), похоже, что обе модели дают разумные результаты. Однако проанализировав все показатели вместе, можно составить довольно точную картину и четко увидеть превосходство модели логистической регрессии.
На следующем шаге мы рассмотрим учет неопределенности.
