На этом шаге мы рассмотрим учет неопределенности.
Матрица ошибок и отчет о результатах классификации позволяют провести очень детальный анализ полученных прогнозов. Однако сами по себе прогнозы лишены большого объема информации, которая собрана моделью. Как мы уже говорили, большинство классификаторов для оценки степени достоверности прогнозов позволяют использовать методы decision_function() или predict_proba(). Получить прогнозы можно, установив для decision_function() или predict_proba() пороговое значение в некоторой фиксированной точке - в случае бинарной классификации мы используем 0 для решающей функции и 0.5 для метода predict_proba().
Ниже приведен пример несбалансированной бинарной классификации: 400 точек данных в отрицательном классе и 50 точек данных в положительном классе. Обучающие данные показаны на рисунке 1 слева. Мы обучаем модель ядерного SVM на этих данных, а также выводим справа графики обучающих данных, показывающие значения решающей функции в виде теплокарты. В самом центре графика можно увидеть черную окружность, который соответствует пороговому значению decision_function, равному нулю. Точки внутри этой окружности будут классифицироваться как положительный класс, а точки вне окружности будут отнесены к отрицательному классу:
[In 51]: from mglearn.datasets import make_blobs X, y = make_blobs(n_samples=(400, 50), centers=2, cluster_std=[7.0, 2], random_state=22) X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) svc = SVC(gamma=.05).fit(X_train, y_train)
[In 52]:
mglearn.plots.plot_decision_threshold()
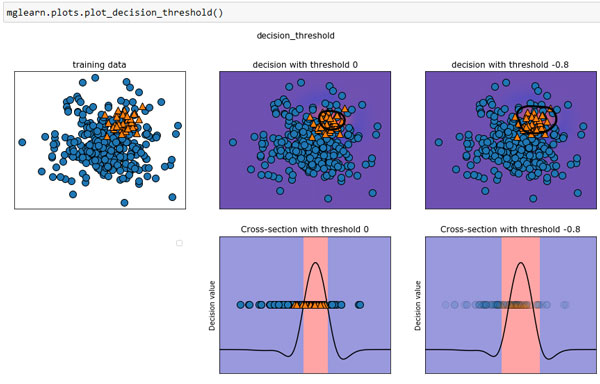
Рис.1. Тепловая карта решающей функции и влияние изменения порогового значения на результат
Воспользуемся функцией classification_report(), чтобы оценить точность и полноту для обоих классов:
[In 53]: print(classification_report(y_test, svc.predict(X_test))) precision recall f1-score support 0 0.97 0.89 0.93 104 1 0.35 0.67 0.46 9 accuracy 0.88 113 macro avg 0.66 0.78 0.70 113 weighted avg 0.92 0.88 0.89 113
Для класса 1 мы получаем довольно небольшое значение полноты и еще более низкое значение точности. Поскольку класс 0 представлен горяздо большим количеством примеров, классификатор точнее прогнозирует класс 0 и гораздо менее точно класс 1.
Давайте предположим, что в нашем примере гораздо важнее получить высокое значение полноты для класса, как в случае со скринингом рака, приведенном ранее. Это означает, что мы готовы допустить большее количество ложных срабатываний (случаев, когда неверно спрогнозирован класс 1), что даст нам большее количество истинно положительных примеров (то есть увеличит значение полноты). Прогнозы, полученные с помощью svc.predict, не отвечают этому требованию, но мы можем скорректировать их, чтобы получить более высокое значение полноты для класса 1. Для этого необходимо изменить пороговое значение для принятия решений. По умолчанию точки данных со значениями решающей функции больше 0 будут классифицироваться как класс 1. Мы хотим увеличить количество точек данных, прогнозируемых как класс 1, поэтому нужно снизить пороговое значение:
[In 54]: y_pred_lower_threshold = svc.decision_function(X_test) > -.8
Давайте взглянем на отчет о результатах классификации, полученный для этого прогноза:
[In 55]: print(classification_report(y_test, y_pred_lower_threshold)) precision recall f1-score support 0 1.00 0.82 0.90 104 1 0.32 1.00 0.49 9 accuracy 0.83 113 macro avg 0.66 0.91 0.69 113 weighted avg 0.95 0.83 0.87 113
Как и следовало ожидать, значение полноты для класса 1 стало высоким, а точность упала. Сейчас для большей области пространства мы прогнозируем класс 1, как это показано в верхней правой части рисунка 1. Если вам нужно увеличить точность по сравнению с полнотой или наоборот, либо ваши данные в значительной степени не сбалансированы, изменение порогового значения является самым простым способом улучшить результат. Поскольку решающая функция может принимать различные диапазоны значений, трудно сформулировать правило, касающееся выбора порогового значения.
Устанавливая пороговое значение, убедитесь в том, что не используете для этого тестовый набор. Как и в случае с любым другим параметром, пороговое значение, выбранное с помощью тестового набора,
вероятно, даст очень оптимистичные результаты. Для выбора порогового значения используйте проверочный набор или перекрестную проверку.
Выбрать пороговое значение для моделей, поддерживающих метод predict_proba(), проще, поскольку выводом predict_proba() являются числа, находящиеся в фиксированном диапазоне от 0 до 1 и представляющие собой вероятности. По умолчанию порог 0.5 означает, что если модель более чем на 50% "уверена", что данная точка является положительным классом, точка будет классифицирована как положительный класс. Повышение порогового значения подразумевает, что модели требуется большая степень уверенности, чтобы принять решение в пользу положительного класса (или меньшая степень уверенности, чтобы принять решение в пользу отрицательного класса). Несмотря на то, что работать с вероятностями проще, чем работать с произвольными пороговыми значениями, не все модели позволяют получить реалистичные оценки неопределенности (например, дерево решений максимальной глубины всегда на 100% уверено в своих прогнозах, хотя это часто не так). Это связано с понятием калибровки (calibration): калиброванная модель представляет собой модель, которая позволяет точно измерить неопределенность оценок. Подробное рассмотрение вопросов калибровки выходит за рамки нашего изложения.
На следующем шаге мы рассмотрим кривые точности-полноты и ROC-кривые.
