На этом шаге мы рассмотрим назначение и построение кривых точности-полноты.
Как мы уже сказали, изменение порога, используемого для классификации решений модели - это способ, позволяющий найти компромисс между точностью и полнотой для данного классификатора. Возможно, вы хотите пропустить менее 10% положительных примеров, таким образом, желаемое значение полноты составит 90%. Решение зависит от конкретного примера и оно должно определяться бизнес-целями. Как только поставлена конкретная цель, скажем, задано конкретное значение полноты или точности для класса, можно установить соответствующий порог. Всегда можно задать то или иное пороговое значение для реализации конкретной цели (например, достижения значения полноты 90%). Трудность состоит в разработке такой модели, которая при этом пороге еще и будет иметь приемлемое значение точности, ведь классифицировав все примеры как положительные, вы получите значение полноты, равное 100%, но при этом ваша модель будет бесполезной.
Требование, выдвигаемое к качеству модели (например, значение полноты должно быть 90%), часто называют рабочей точкой (operating point). Фиксирование рабочей точки часто бывает полезно в контексте бизнеса, чтобы гарантировать определенный уровень качества клиентам или другим группам лиц внутри организации.
Как правило, при разработке новой модели нет четкого представления о том, что будет рабочей точкой. По этой причине, а также для того, чтобы получить более полное представление о решаемой задаче, полезно сразу взглянуть на все возможные пороговые значения или все возможные соотношения точности и полноты для этих пороговых значений. Данную процедуру можно осуществить с помощью инструмента, называемого кривой точности-полноты (precision-recall curve). Функцию для вычисления кривой точности-полноты можно найти в модуле sklearn.metrics. Ей необходимо передать фактические метки классов и спрогнозированные вероятности, вычисленные с помощью decision_function() или predict_proba():
[In 56]: from sklearn.metrics import precision_recall_curve precision, recall, thresholds = precision_recall_curve( y_test, svc.decision_function(X_test))
Функция precision_recall_curve() возвращает список значений точности и полноты для всех возможных пороговых значений (всех значений решающей функции) в отсортированном виде, поэтому мы можем построить кривую, как показано на рисунке 1:
[In 57]: # используем больший объем данных, чтобы получить более гладкую кривую X, y = make_blobs(n_samples=(4000, 500), centers=2, cluster_std=[7.0, 2], random_state=22) X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) svc = SVC(gamma=.05).fit(X_train, y_train) precision, recall, thresholds = precision_recall_curve( y_test, svc.decision_function(X_test)) # находим ближайший к нулю порог close_zero = np.argmin(np.abs(thresholds)) plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10, label="порог 0", fillstyle="none", c='k', mew=2) plt.plot(precision, recall, label="кривая точности-полноты") plt.xlabel("Точность") plt.ylabel("Полнота") plt.legend(loc="best")
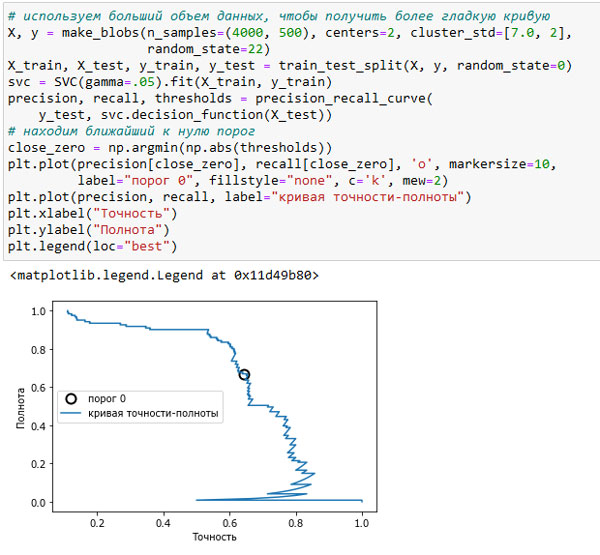
Рис.1. Кривая точности-полноты для SVC (gamma=0.05)
Каждая точка на кривой (рисунок 1) соответствует возможному пороговому значению решающей функции. Например, видно, что мы можем достичь полноты 0.4 при точности около 0.75. Черный кружок отмечает точку, соответствующую порогу 0, пороговому значению по умолчанию для решающей функции. Данная точка является компромиссом, который выбирается при вызове метода predict().
Чем ближе кривая подходит к верхнему правом углу, тем лучше классификатор. Точка в верхнем правом углу означает высокое значение точности и высокое значение полноты для соответствующего порога. Кривая начинается в верхнем левом углу, что соответствует очень низкому порогу, все примеры классифицируются как положительный класс. Повышение порога перемещает кривую в сторону более высоких значений точности и в то же время более низких значений полноты. При дальнейшем повышении порога мы получаем ситуацию, в которой большинство точек, классифицированных как положительные, являются истинно пложительными, что приводит к очень высокой точности, но более низкому значению полноты. Чем больше модель сохраняет высокое значение полноты при одновременном увеличении точности, тем лучше.
Взглянув на эту кривую чуть более пристально, можно увидеть, что с помощью построенной модели можно добиться точности в районе 0.5 при очень высоком значении полноты. Если мы хотим получить гораздо более высокое значение точности, мы должны в значительной степени пожертвовать полнотой. Другими словами, слева наша кривая выглядит относительно плоской, это означает, что при увеличении точности полнота падает незначительно. Однако, чтобы получить значение точности более 0.5, нам придется пожертвовать значительным снижением полноты.
На следующем шаге мы закончим изучение этого вопроса.
