На этом шаге мы рассмотрим использование ROC-кривых.
Различные классификаторы могут давать хорошее качество на различных участках кривой, то есть в разных рабочих точках. Давайте сравним модель SVM с моделью случайного леса, построенной на том же наборе данных. RandomForestClassifier вместо decision_function использует метод predict_proba(). Функция precision_recall_curve() ожидает, что в качестве второго аргумента ей будет передана вероятность положительного класса (класса 1), то есть rf.predict_proba(X_test)[:, 1]. В бинарной классификации пороговое значение по умолчанию для predict_proba() равно 0.5, поэтому мы отметили эту точку на кривой (см. рисунок 1):
[In 58]: from sklearn.ensemble import RandomForestClassifier rf = RandomForestClassifier(n_estimators=100, random_state=0, max_features=2) rf.fit(X_train, y_train) # в RandomForestClassifier есть predict_proba, но нет decision_function precision_rf, recall_rf, thresholds_rf = precision_recall_curve( y_test, rf.predict_proba(X_test)[:, 1]) plt.plot(precision, recall, label="svc") plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10, label="порог 0 svc", fillstyle="none", c='k', mew=2) plt.plot(precision_rf, recall_rf, label="rf") close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5)) plt.plot(precision_rf[close_default_rf], recall_rf[close_default_rf], '^', c='k', markersize=10, label="порог 0.5 rf", fillstyle="none", mew=2) plt.xlabel("Точность") plt.ylabel("Полнота") plt.legend(loc="best")
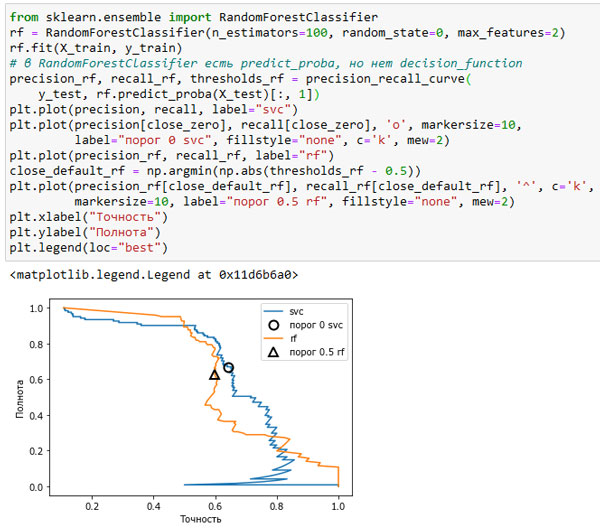
Рис.1. Сравнение кривых точности-полноты для SVM и случайного леса
Из сравнительного графика видно, что случайный лес дает лучшее качество, чем в SVM, для крайних пороговых значений, позволяя получить очень высокое значение точности или очень высокое значение полноты. Что касается центральной части кривой (соответствует примерной точности=0.7), то SVM работает лучше. Если бы мы для сравнения обобщающей способности в целом анализировали лишь f1-меру, мы упустили бы из виду эти тонкости. f1-мера учитывает только одну точку на кривой точности-полноты, точку, определяемую порогом по умолчанию.
[In 59]: print("f1-мера random forest: {:.3f}".format( f1_score(y_test, rf.predict(X_test)))) print("f1-мера svc: {:.3f}".format(f1_score(y_test, svc.predict(X_test)))) f1-мера random forest: 0.610 f1-мера svc: 0.656
Сравнение двух кривых точности-полноты дает много детальной информации, но представляет собой довольно трудоемкий процесс. Чтобы выполнить автоматическое сравнение моделей мы могли бы обобщить информацию, содержащуюся в кривой, не ограничиваясь конкретным пороговым значением или рабочей точкой. Один из способов подытожить информацию кривой заключается в вычислении интеграла или площади под кривой точности-полноты, он также известен как метод средней точности (average precision).
С технической точки зрения существует некоторые незначительные различия между площадью под кривой точности-полноты и средней точностью. Однако приведенное объяснение передает общую идею.
Для вычисления средней точности вы можете воспользоваться функцией average_precision_score(). Поскольку нам нужно вычислить ROC-кривую и рассмотреть несколько пороговых значений, функции average_precision_score() вместо результата predict() нужно передать результат decision_function() или predict_proba():
[In 60]: from sklearn.metrics import average_precision_score ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1]) ap_svc = average_precision_score(y_test, svc.decision_function(X_test)) print("Средняя точность random forest: {:.3f}".format(ap_rf)) print("Средняя точность svc: {:.3f}".format(ap_svc)) Средняя точность random forest: 0.660 Средняя точность svc: 0.666
При усреднении по всем возможным пороговым значением мы видим, что случайный лес и SVC дают примерно одинаковое качество модели, при этом случайный даже чуть-чуть вырывается вперед. Это в значительном мере отличаются от результата, полученного нами ранее с помощью f1_score. Поскольку средняя точность равна площади под кривой, которая принимает значения от 0 до 1, средняя точность всегда возвращает значение от 0 (худшее значение) до 1 (лучшее значение). Средняя точность случайного классификатора равна доле положительных примеров в наборе данных.
На следующем шаге мы рассмотрим рабочую характеристику приемника (ROC) и AUC.
