На этом шаге мы рассмотрим формирование и использование ROC-кривой.
Еще один инструмент, который обычно используется для анализа поведения классификаторов при различных пороговых значениях - это кривая рабочей характеристики приемника (receiver operating characteristics curve) или кратко ROC-кривая (ROC curve). Как и кривая точности-полноты, ROC-кривая позволяет рассмотреть все пороговые значения для данного классификатора, но вместо точности и полноты она показывает долю ложно положительных примеров (false positive rate, FPR) в сравнении с долей истинно положительных примеров (true positive rate). Вспомним, что доля истинно положительных примеров - это просто еще одно название полноты, тогда как доля ложно положительных примеров - это доля ложно положительных примеров от общего количества отрицательных примеров:
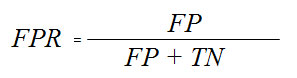
ROC-кривую можно вычислить с помощью функции roc_curve() (см. рисунок 1):
[In 61]: from sklearn.metrics import roc_curve fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test)) plt.plot(fpr, tpr, label="ROC-кривая") plt.xlabel("FPR") plt.ylabel("TPR (полнота)") # находим пороговое значение, ближайшее к нулю close_zero = np.argmin(np.abs(thresholds)) plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label="порог 0", fillstyle="none", c='k', mew=2) plt.legend(loc=4)
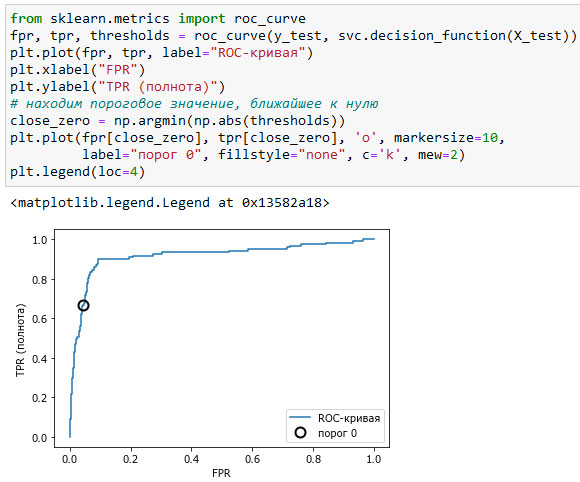
Рис.1. ROC-кривая для SVM
Идеальная ROC-кривая проходит через левый верхний угол, соответствуя классификатору, который дает высокое значение полноты при низкой доле ложно положительных примеров. Проанализировав значения полноты и FPR для порога по умолчанию 0, мы видим, что можем достичь гораздо более высокого значения полноты (около 0.9) лишь при незначительном увеличении FPR. Точка, ближе всего расположенная к верхнему левому углу, возможно, будет лучшей рабочей точкой, чем та, что выбрана по умолчанию. Опять же, имейте в виду, что для выбора порогового значения следовать использовать отдельный проверочный набор, а не тестовые данные.
На рисунке 2 вы можете сравнить случайный лес и SVM с помощью ROC-кривых:
[In 62]: from sklearn.metrics import roc_curve fpr_rf, tpr_rf, thresholds_rf = roc_curve(y_test, rf.predict_proba(X_test)[:, 1]) plt.plot(fpr, tpr, label="ROC-кривая SVC") plt.plot(fpr_rf, tpr_rf, label="ROC-кривая RF") plt.xlabel("FPR") plt.ylabel("TPR (полнота)") plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label="порог 0 SVC", fillstyle="none", c='k', mew=2) close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5)) plt.plot(fpr_rf[close_default_rf], tpr[close_default_rf], '^', markersize=10, label="порог 0.5 RF", fillstyle="none", c='k', mew=2) plt.legend(loc=4)
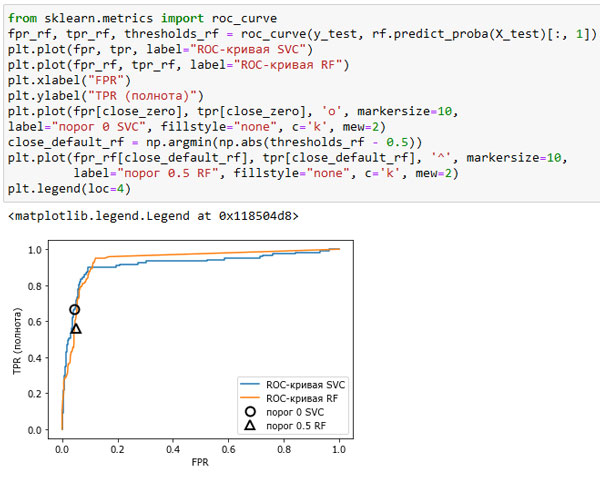
Рис.2. Сравнение ROC-кривых для SVM и случайного леса
Как и в случае с кривой точности-полноты, мы хотим подытожить информацию ROC-кривой с помощью одного числа, площади под кривой (обычно ее просто называют AUC, при этом имейте в виду, что речь идет о ROC-кривой). Мы можем вычислить площадь под ROC-кривой с помощью функции roc_auc_score():
[In 63]: from sklearn.metrics import roc_auc_score rf_auc = roc_auc_score(y_test, rf.predict_proba(X_test)[:, 1]) svc_auc = roc_auc_score(y_test, svc.decision_function(X_test)) print("AUC для случайного леса: {:.3f}".format(rf_auc)) print("AUC для SVC: {:.3f}".format(svc_auc)) AUC для случайного леса: 0.937 AUC для SVC: 0.916
На следующем шаге мы закончим изучение этого вопроса.
