На этом шаге мы рассмотрим, как они влияют на результаты обучения.
Если вы в своей жизни видели только двух рыжих полосатых кошек и обе они были жутко агрессивными, вы можете сделать вывод, что рыжие полосатые кошки, как правило, агрессивны. Перед вами наглядный пример переобучения: если бы вы встретили большее количество кошек, и не только рыжих, то узнали бы, что характер кошки на самом деле не зависит от ее окраски.
Точно так же модели машинного обучения, натренированные на наборах данных, включающих редкие значения признаков, подвержены переобучению. Если в задаче классификации отзывов в одном из текстов обучающей выборки появится слово cherimoya (черимойя - плод, произрастающий в Андах), а отзыв будет отрицательным, то слабо регуляризованная модель может придать этому слову слишком большой вес - и всегда относить к отрицательным любые новые отзывы, упоминающие черимойю, тогда как объективно в этой ягоде нет ничего плохого.
Важно отметить, что значение признака не обязательно должно встречаться всего несколько раз, чтобы породить ложные корреляции. Представьте слово, которое появляется в ста обучающих образцах, из которых 54% имеют положительную оценку, а 46% - отрицательную. Эта разница вполне может быть обусловлена статистической погрешностью, но модель, весьма вероятно, научится использовать данный признак для решения задачи классификации. Это один из самых распространенных источников переобучения.
Вот яркий пример. Возьмем набор MNIST. Создадим новую обучающую выборку, добавив к существующему 784-мерному измерению с фактическими данными такое же 784-мерное измерение с белым шумом, чтобы белый шум занимал половину данных. Для сравнения создадим эквивалентную выборку, добавив 784-мерное измерение с нулями. Добавление бессмысленных признаков никак не влияет на информационное содержание данных: просто в выборке появились измерения, не несущие никакой информации. Эти дополнения никак не повлияют на способность человека различать рукописные цифры.
Пример 5.1. Добавление пустых признаков и признаков с белым шумом в выборку с данными из набора MNIST
from tensorflow.keras.datasets import mnist import numpy as np (train_images, train_labels), _ = mnist.load_data() train_images = train_images.reshape((60000, 28 * 28)) train_images = train_images.astype("float32") / 255 train_images_with_noise_channels = np.concatenate( [train_images, np.random.random((len(train_images), 784))], axis=1) train_images_with_zeros_channels = np.concatenate( [train_images, np.zeros((len(train_images), 784))], axis=1)
Теперь натренируем ранее созданную модель на обеих обучающих выборках.
Пример 5.2. Обучение модели на выборке, включающей пустые признаки и признаки с белым шумом
from tensorflow import keras from tensorflow.keras import layers def get_model(): model = keras.Sequential([ layers.Dense(512, activation="relu"), layers.Dense(10, activation="softmax") ]) model.compile(optimizer="rmsprop", loss="sparse_categorical_crossentropy", metrics=["accuracy"]) return model model = get_model() history_noise = model.fit( train_images_with_noise_channels, train_labels, epochs=10, batch_size=128, validation_split=0.2) model = get_model() history_zeros = model.fit( train_images_with_zeros_channels, train_labels, epochs=10, batch_size=128, validation_split=0.2)
И посмотрим, как изменяется точность обеих моделей на проверочной выборке в процессе обучения.
Пример 5.3. Вывод сравнительного графика изменения точности моделей на проверочной выборке
import matplotlib.pyplot as plt val_acc_noise = history_noise.history["val_accuracy"] val_acc_zeros = history_zeros.history["val_accuracy"] epochs = range(1, 11) plt.plot(epochs, val_acc_noise, "b-", label="Точность проверки с белым шумом") plt.plot(epochs, val_acc_zeros, "b--", label="Точность проверки с пустыми признаками") plt.title("Влияние признаков с белым шумом на точность проверки") plt.xlabel("Эпохи") plt.ylabel("Точность") plt.legend()
Блокнот с примером "белого шума" можно взять здесь.
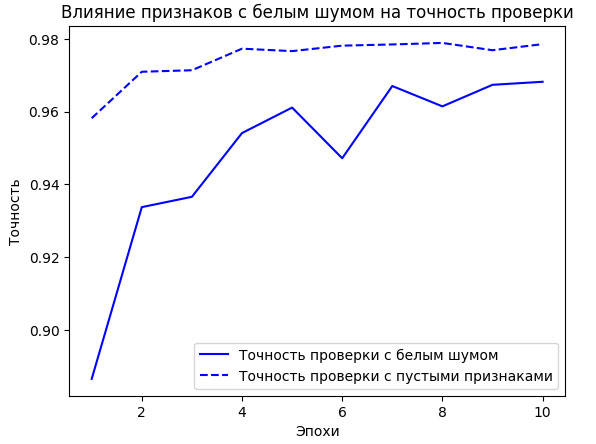
Рис.1. Влияние признаков с белым шумом на точность проверки
Несмотря на то что обе выборки содержат одну и ту же информацию, точность модели, обученной на выборке с белым шумом, оказалась примерно на один процент ниже (рисунок 1) - очевидно, что это отставание обусловлено влиянием ложных корреляций. Чем больше каналов с шумом будет добавлено в выборку, тем хуже будет точность.
Зашумленные признаки неуклонно ведут к переобучению. Поэтому, когда нет четкой уверенности в информативности признаков, перед обучением прибегают к отбору признаков. Например, ограничение данных из IMDB десятью тысячами самых распространенных слов было упрощенной формой отбора признаков. Типичный способ отобрать признаки - вычислить некоторую оценку полезности для каждого доступного признака, показывающую, насколько он информативен для решаемой задачи (например, тесноту связи между признаком и метками), и оставить только признаки с оценкой выше некоторого порога. Это поможет отфильтровать неинформативные признаки, такие как канал с белым шумом в предыдущем примере.
На следующем шаге мы рассмотрим природу общности в глубоком обучении.
