На этом шаге мы рассмотрим смысл выполнения этой операции.
Ранее мы улучшали поведение простого линейного классификатора путем регулирования параметра наклона линейной функции узла. Мы делали это, руководствуясь текущей величиной ошибки, т.е. разности между ответом, вырабатываемым узлом, и известным нам истинным значением. Ввиду простоты соотношения между величинами ошибки и поправки это было несложно.
Как нам обновлять весовые коэффициенты связей в случае, если выходной сигнал и его ошибка формируются за счет вкладов более чем одного узла? Эту задачу иллюстрирует приведенная ниже диаграмма.
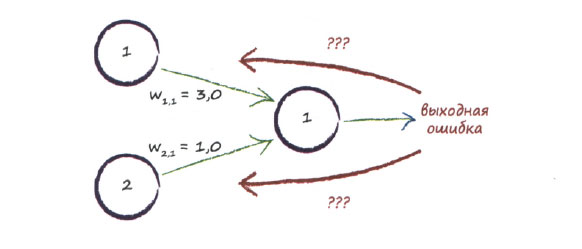
Когда на выходной узел поступал сигнал только от одного узла, все было намного проще. Но как использовать ошибку выходного сигнала при наличии двух входных узлов?
Использовать всю величину ошибки для обновления только одного весового коэффициента не представляется разумным, поскольку при этом полностью игнорируются другая связь и ее вес. Но ведь величина ошибки определяется вкладами всех связей, а не только одной.
Правда, существует небольшая вероятность того, что за ошибку ответственна только одна связь, но эта вероятность пренебрежимо мала. Если мы изменили весовой коэффициент, уже имеющий "правильное" значение, и тем самым ухудшили его, то при выполнении нескольких последующих итераций он должен улучшиться, так что не все потеряно.
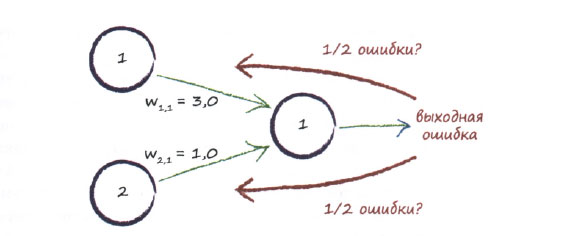
Один из возможных способов состоит в том, чтобы распределить ошибку поровну между всеми узлами, вносящими вклад, как показано на следующей диаграмме.
Суть другой идеи также заключается в том, чтобы распределять ошибку между узлами, однако это распределение не обязано быть равномерным. Вместо этого большая доля ошибки приписывается вкладам тех связей, которые имеют больший вес. Почему? Потому что они оказывают большее влияние на величину ошибки. Эту идею иллюстрирует следующая диаграмма.
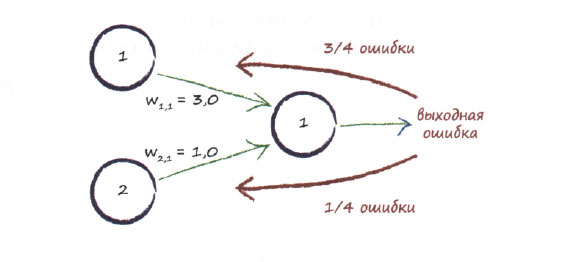
В данном случае сигнал, поступающий на выходной узел, формируется за счет двух узлов. Весовые коэффициенты связей равны 3,0 и 1,0. Распределив ошибку между двумя узлами пропорционально их весам, вы увидите, что для обновления значения первого, большего веса следует использовать 3/4 величины ошибки, тогда как для обновления значения второго, меньшего веса - 1/4.
Мы можем расширить эту идею на случаи с намного большим количеством узлов. Если бы выходной узел был связан со ста входными узлами, мы распределили бы выходную ошибку между всеми ста связями пропорционально их вкладам, размер которых определяется весами соответствующих связей.
Как вы могли заметить, мы используем весовые коэффициенты в двух целях. Во-первых, они учитываются при расчете распространения сигналов по нейронной сети от входного слоя до выходного. Мы интенсивно использовали их ранее именно в таком качестве. Во-вторых, мы используем веса для распространения ошибки в обратном направлении - от выходного слоя вглубь сети. Думаю, вы не будете удивлены, узнав, что этот метод называется обратным распространением ошибки (обратной связью) в процессе обучения нейронной сети.
Если бы выходной слой имел два узла, мы повторили бы те же действия и для второго узла. Второй выходной узел будет характеризоваться собственной ошибкой, распределяемой аналогичным образом между соответствующим количеством входных узлов. Теперь продолжим наше рассмотрение.
На следующем шаге мы рассмотрим обратное распространение ошибок.
