На этом шаге мы рассмотрим пример обратного распространения ошибок в простой нейронной сети.
На следующей диаграмме отображена простая сеть с двумя входными узлами, но на этот раз с двумя выходными узлами.
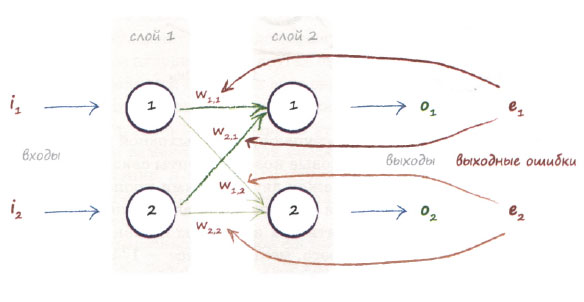
Ошибка может формироваться на обоих узлах - фактически эта ситуация очень похожа на ту, которая возникает, когда сеть еще не обучалась. Вы видите, что для коррекции весов внутренних связей нужна информация об ошибках в обоих узлах. Мы можем использовать прежний подход и распределять ошибку выходного узла между связанными с ним узлами пропорционально весовым коэффициентам соответствующих связей.
В действительности тот факт, что сейчас имеется более чем один выходной узел, ничего не меняет. Мы просто повторяем для второго узла те же действия, которые уже выполняли для первого. Почему все так просто? Эта простота объясняется тем, что связи одного выходного узла не зависят от связей другого. Между этими двумя наборами связей отсутствует какая-либо зависимость.
Вернемся к диаграмме, на которой ошибка на первом выходном узле обозначена как е1. Не забывайте, что это разность между желаемым значением, предоставляемым тренировочными данными t1, и фактическим выходным значением o1. Таким образом, е1 = (t1 - о1). Ошибка на втором выходном узле обозначена как е2.
На диаграмме видно, что ошибка е1 распределяется пропорционально весам связей, обозначенным как w11 и w21. Точно так же ошибка е2 должна распределяться пропорционально весам w12 и w22.
Чтобы у вас не возникало никаких сомнений в правильности получаемых результатов, запишем эти доли в явном виде. Ошибка е1 информирует о величинах поправок для весов w11 и w21. При ее распределении между узлами доля е1, информация о которой используется для обновления w11, определяется следующим выражением:
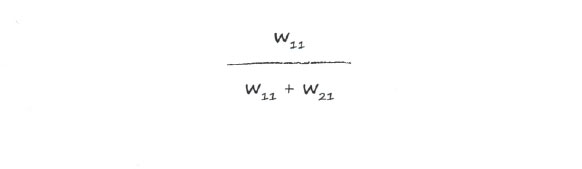
Доля е1, используемая для обновления w21, определяется аналогичным выражением:
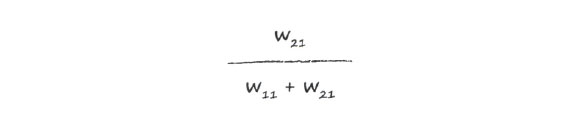
Возможно, эти выражения несколько смущают вас, поэтому рассмотрим их более подробно. За всеми этими символами стоит очень простая идея, которая заключается в том, что узлы, сделавшие больший вклад в ошибочный ответ, получают больший сигнал об ошибке, тогда как узлы, сделавшие меньший вклад, получают меньший сигнал.
Если w11 в два раза превышает w21 (скажем, w11 = 6, a w21 = 3), то доля e1, используемая для обновления w11, составляет 6 / (6+3) = 6/9 = 2/3. Тогда для другого, меньшего веса w21 должно остаться (1/3) * е1, что можно подтвердить с помощью выражения 3(6+З) = 3/9, результат которого действительно авен 1/3.
Как и следовало ожидать, при равных весах будут равны и соответствующие доли. Давайте в этом убедимся. Пусть w11 = 4 и w21 = 4, тогда в обоих случаях доля будет составлять 4(4+4) = 4/8 = 1/2.
Прежде чем продолжить, сделаем паузу и вернемся на шаг назад, чтобы оценить то, что мы уже успели сделать. Мы знали, что при определении величины поправок для некоторых внутренних параметров сети, в данном случае - весов связей, необходимо использовать величину ошибки. Вы видели, как это делается для весов, которые сглаживают входные сигналы последнего, выходного слоя нейронной сети. Вы также видели, что увеличение количества выходных узлов не усложняет задачу, поскольку мы повторяем одни и те же действия для каждого выходного узла. Замечательно!
Но как быть, если количество слоев превышает два? Как обновлять веса связей для слоев, далеко отстоящих от последнего, выходного слоя?
На следующем шаге мы продолжим изучение этого вопроса.
